Question Number 128193 by Algoritm last updated on 05/Jan/21
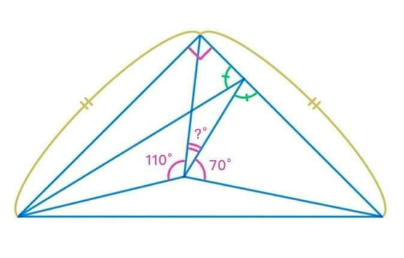
Answered by mr W last updated on 05/Jan/21

Commented by Algoritm last updated on 05/Jan/21

$$?=\:\: \\ $$
Commented by mr W last updated on 05/Jan/21

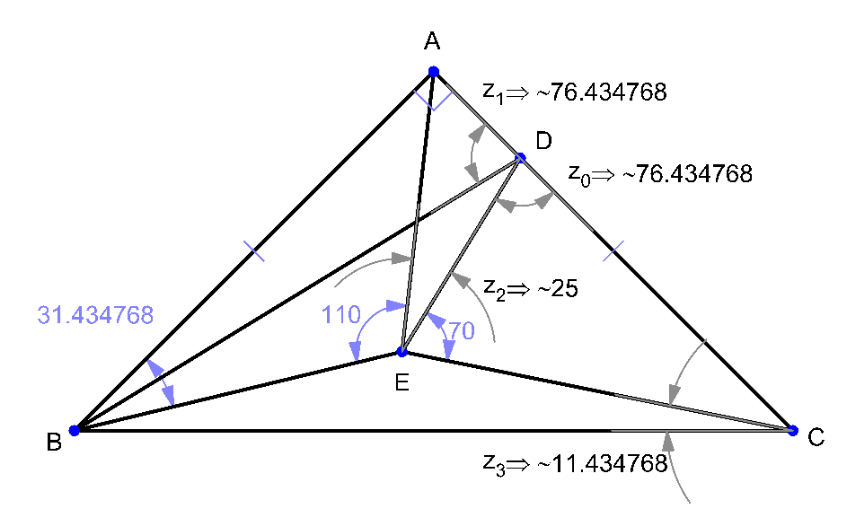
$$\frac{{AE}}{\mathrm{sin}\:\beta}=\frac{{BE}}{\mathrm{sin}\:\left(\mathrm{110}+\beta\right)}=\frac{{AB}}{\mathrm{sin}\:\mathrm{110}} \\ $$$$\Rightarrow{AE}=\frac{\mathrm{sin}\:\beta}{\mathrm{sin}\:\mathrm{70}} \\ $$$$\Rightarrow{BE}=\frac{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}{\mathrm{sin}\:\mathrm{70}} \\ $$$$\frac{{EC}}{\mathrm{sin}\:\left(\mathrm{45}−\beta\right)}=\frac{{BC}}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)}=\frac{{BE}}{\mathrm{sin}\:\gamma} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)}=\frac{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}{\mathrm{sin}\:\mathrm{70}\:\mathrm{sin}\:\gamma} \\ $$$$\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{70}}{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}=\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\beta−\gamma\right)−\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\beta−\gamma\right)}{\mathrm{2}\:\mathrm{sin}\:\gamma} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{70}}{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}=\frac{\mathrm{cos}\:\left(\beta−\gamma\right)−\mathrm{sin}\:\left(\beta−\gamma\right)}{\mathrm{sin}\:\gamma} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{70}}{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}=\frac{\mathrm{cos}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma−\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma}{\mathrm{sin}\:\gamma} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{70}}{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}=\mathrm{sin}\:\beta+\mathrm{cos}\:\beta+\frac{\mathrm{cos}\:\beta−\mathrm{sin}\:\beta}{\mathrm{tan}\:\gamma} \\ $$$$\Rightarrow\mathrm{tan}\:\gamma=\frac{\mathrm{cos}\:\beta−\mathrm{sin}\:\beta}{\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{70}}{\mathrm{sin}\:\left(\mathrm{70}−\beta\right)}−\mathrm{sin}\:\beta−\mathrm{cos}\:\beta}\:\:\:…\left({i}\right) \\ $$$${EC}=\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{45}−\beta\right)}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)} \\ $$$$\alpha=\mathrm{180}−\mathrm{70}−\left(\mathrm{45}−\gamma\right)=\mathrm{65}+\gamma \\ $$$${AD}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{65}+\gamma\right)} \\ $$$${DC}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{65}+\gamma\right)} \\ $$$$\frac{{DC}}{\mathrm{sin}\:\mathrm{70}}=\frac{{EC}}{\mathrm{sin}\:\alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{70}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{65}+\gamma\right)}\right)=\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{45}−\beta\right)}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)\mathrm{sin}\:\left(\mathrm{65}+\gamma\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{70}}\left(\mathrm{sin}\:\left(\mathrm{65}+\gamma\right)−\mathrm{cos}\:\left(\mathrm{65}+\gamma\right)\right)=\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{45}−\beta\right)}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{65}+\gamma\right)−\mathrm{cos}\:\left(\mathrm{65}+\gamma\right)=\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{70}\:\mathrm{sin}\:\left(\mathrm{45}−\beta\right)}{\mathrm{sin}\:\left(\mathrm{45}−\beta+\gamma\right)}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\beta=\mathrm{31}.\mathrm{434768}°,\:\gamma=\mathrm{11}.\mathrm{434768}° \\ $$$$?=\mathrm{45}−\beta+\gamma=\mathrm{25}° \\ $$
Commented by mr W last updated on 05/Jan/21

$${here}\:{a}\:{check}: \\ $$
Commented by mr W last updated on 05/Jan/21
Commented by Algoritm last updated on 06/Jan/21

$$\mathrm{thanks} \\ $$
