Question Number 128194 by Algoritm last updated on 05/Jan/21
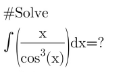
Commented by MJS_new last updated on 05/Jan/21
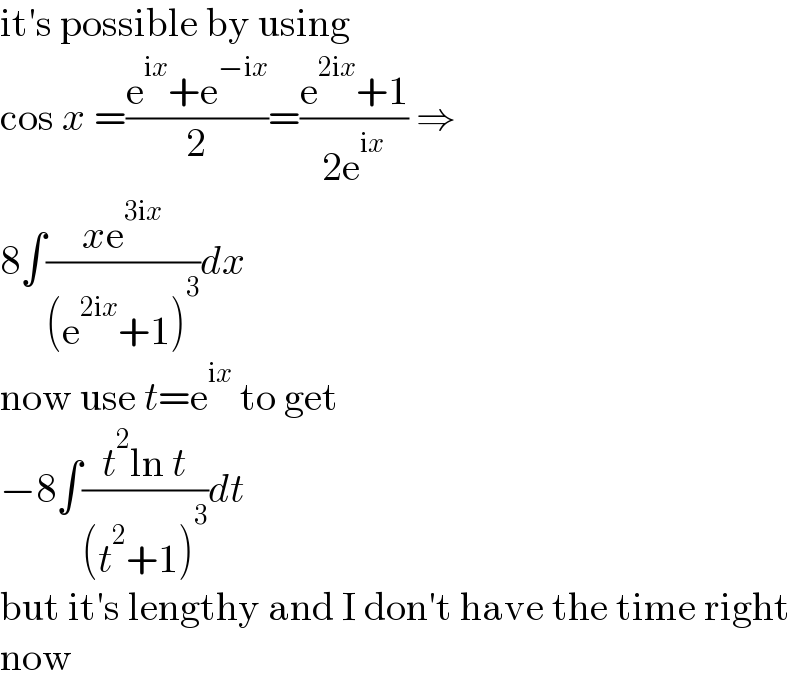
$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{by}\:\mathrm{using} \\ $$$$\mathrm{cos}\:{x}\:=\frac{\mathrm{e}^{\mathrm{i}{x}} +\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}=\frac{\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}}{\mathrm{2e}^{\mathrm{i}{x}} }\:\Rightarrow \\ $$$$\mathrm{8}\int\frac{{x}\mathrm{e}^{\mathrm{3i}{x}} }{\left(\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$$\mathrm{now}\:\mathrm{use}\:{t}=\mathrm{e}^{\mathrm{i}{x}} \:\mathrm{to}\:\mathrm{get} \\ $$$$−\mathrm{8}\int\frac{{t}^{\mathrm{2}} \mathrm{ln}\:{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt} \\ $$$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{lengthy}\:\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{the}\:\mathrm{time}\:\mathrm{right} \\ $$$$\mathrm{now} \\ $$
Commented by MJS_new last updated on 06/Jan/21
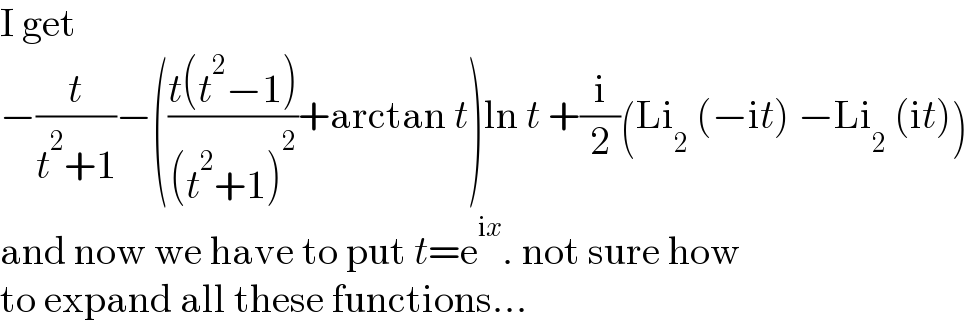
$$\mathrm{I}\:\mathrm{get} \\ $$$$−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}−\left(\frac{{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{arctan}\:{t}\right)\mathrm{ln}\:{t}\:+\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{Li}_{\mathrm{2}} \:\left(−\mathrm{i}{t}\right)\:−\mathrm{Li}_{\mathrm{2}} \:\left(\mathrm{i}{t}\right)\right) \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{put}\:{t}=\mathrm{e}^{\mathrm{i}{x}} .\:\mathrm{not}\:\mathrm{sure}\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{expand}\:\mathrm{all}\:\mathrm{these}\:\mathrm{functions}… \\ $$
Answered by chengulapetrom last updated on 05/Jan/21
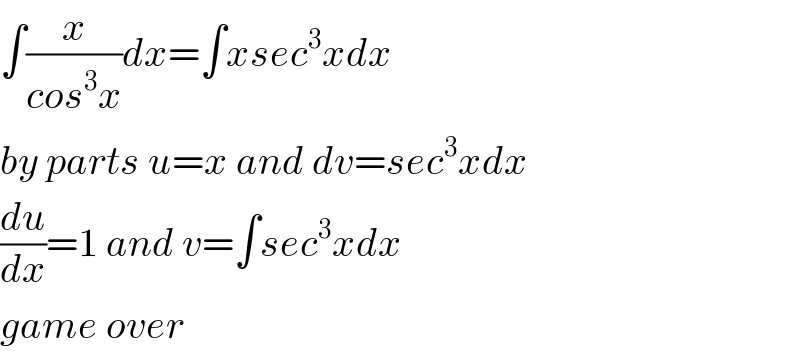
$$\int\frac{{x}}{{cos}^{\mathrm{3}} {x}}{dx}=\int{xsec}^{\mathrm{3}} {xdx} \\ $$$${by}\:{parts}\:{u}={x}\:{and}\:{dv}={sec}^{\mathrm{3}} {xdx} \\ $$$$\frac{{du}}{{dx}}=\mathrm{1}\:{and}\:{v}=\int{sec}^{\mathrm{3}} {xdx} \\ $$$${game}\:{over} \\ $$
