Question Number 128254 by Ahmed1hamouda last updated on 05/Jan/21
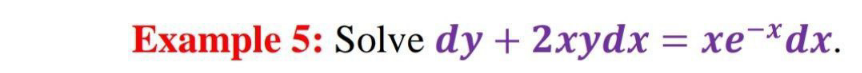
Answered by mr W last updated on 06/Jan/21
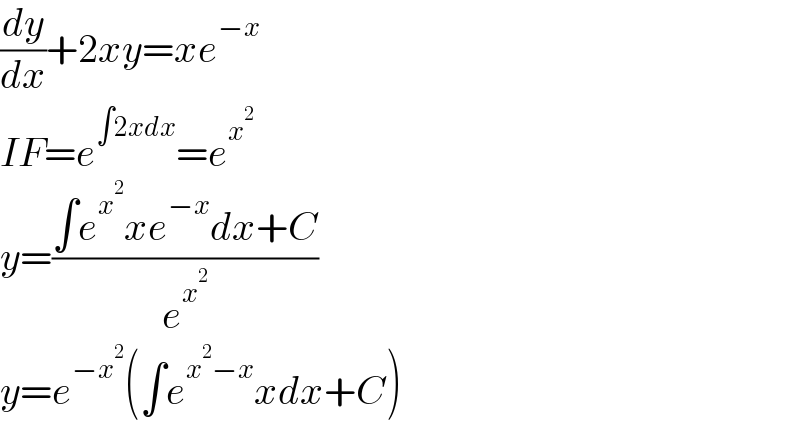
$$\frac{{dy}}{{dx}}+\mathrm{2}{xy}={xe}^{−{x}} \\ $$$${IF}={e}^{\int\mathrm{2}{xdx}} ={e}^{{x}^{\mathrm{2}} } \\ $$$${y}=\frac{\int{e}^{{x}^{\mathrm{2}} } {xe}^{−{x}} {dx}+{C}}{{e}^{{x}^{\mathrm{2}} } } \\ $$$${y}={e}^{−{x}^{\mathrm{2}} } \left(\int{e}^{{x}^{\mathrm{2}} −{x}} {xdx}+{C}\right) \\ $$
