Question-128303

Question Number 128303 by mr W last updated on 06/Jan/21

Commented by mr W last updated on 06/Jan/21

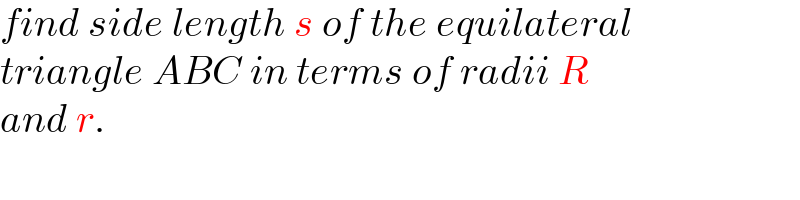
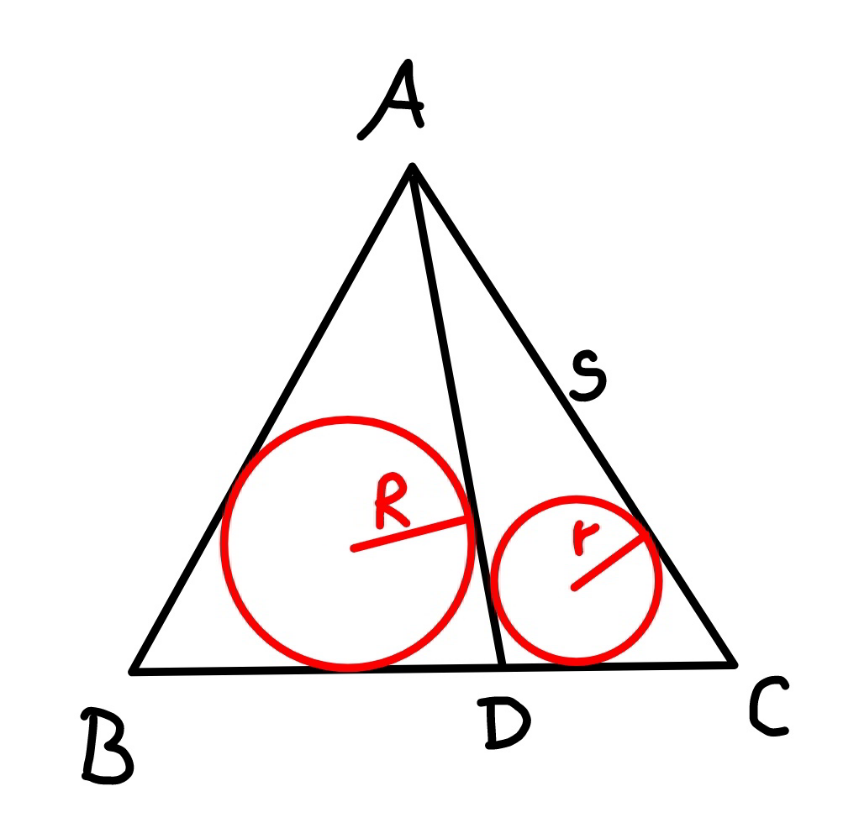
$${find}\:{side}\:{length}\:{s}\:{of}\:{the}\:{equilateral} \\ $$$${triangle}\:{ABC}\:{in}\:{terms}\:{of}\:{radii}\:{R} \\ $$$${and}\:{r}. \\ $$

Commented by mr W last updated on 06/Jan/21

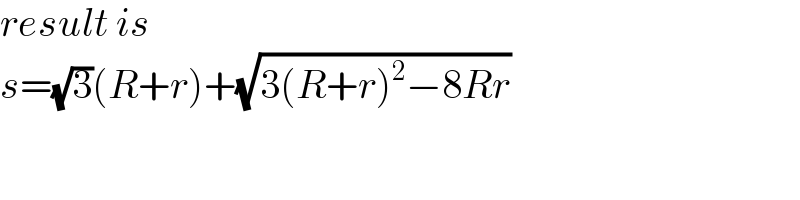
result is s=(√3)(R+r)+(√(3(R+r)^2 −8Rr))

$${result}\:{is} \\ $$$${s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\sqrt{\mathrm{3}\left({R}+{r}\right)^{\mathrm{2}} −\mathrm{8}{Rr}} \\ $$

Answered by mr W last updated on 06/Jan/21

Commented by mr W last updated on 07/Jan/21

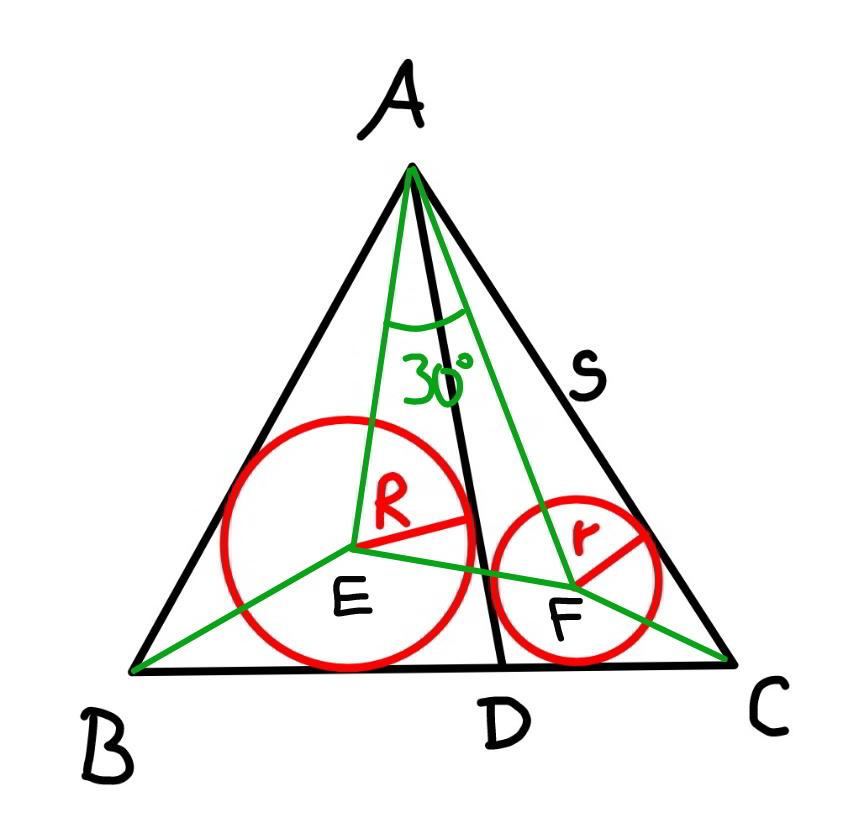
AE^2 =(s−(√3)R)^2 +R^2 =s^2 −2(√3)Rs+4R^2 AF^2 =(s−(√3)r)^2 +r^2 =s^2 −2(√3)rs+4r^2 EF^2 =(s−(√3)R−(√3)r)^2 +(R−r)^2 =s^2 −2(√3)(R+r)+4(R^2 +r^2 +Rr) EF^2 =AE^2 +AF^2 −2×AE×AF×cos 30° (s−(√3)R−(√3)r)^2 +(R−r)^2 =(s−(√3)R)^2 +R^2 +(s−(√3)r)^2 +r^2 −(√(3[(s−(√3)R)^2 +R^2 ][(s−(√3)r)^2 +r^2 ])) s^2 −2(√3)(R+r)+4(R^2 +r^2 +Rr)=s^2 −2(√3)Rs+4R^2 +s^2 −2(√3)rs+4r^2 −(√(3(s^2 −2(√3)Rs+4R^2 )(s^2 −2(√3)rs+4r^2 ))) s^2 −4Rr=(√(3(s^2 −2(√3)Rs+4R^2 )(s^2 −2(√3)rs+4r^2 ))) (s^2 −4Rr)^2 =3(s^2 −2(√3)Rs+4R^2 )(s^2 −2(√3)rs+4r^2 ) s^4 −3(√3)(R+r)s^3 +2(3R^2 +3r^2 +11Rr)s^2 −12(√3)Rr(R+r)s+16R^2 r^2 =0 9((s/( (√3))))^4 −27(R+r)((s/( (√3))))^3 +6(3R^2 +3r^2 +11Rr)((s/( (√3))))^2 −36Rr(R+r)((s/( (√3))))+16R^2 r^2 =0 let t=(s/( (√3))) ⇒9t^4 −27(R+r)t^3 +6(3R^2 +3r^2 +11Rr)t^2 −36Rr(R+r)t+16R^2 r^2 =0 ⇒[3t^2 −6(R+r)t+8Rr][3t^2 −3(R+r)t+2Rr]=0 ⇒t=R+r+(1/( (√3)))(√(3(R+r)^2 −8Rr)) ⇒s=(√3)(R+r)+(√(3(R+r)^2 −8Rr)) example: R=3, r=2 s=(√3)(3+2)+(√(3×(3+2)^2 −8×3×2)) =5(√3)+3(√3) =8(√3) ✓

$${AE}^{\mathrm{2}} =\left({s}−\sqrt{\mathrm{3}}{R}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} ={s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{Rs}+\mathrm{4}{R}^{\mathrm{2}} \\ $$$${AF}^{\mathrm{2}} =\left({s}−\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} ={s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{rs}+\mathrm{4}{r}^{\mathrm{2}} \\ $$$${EF}^{\mathrm{2}} =\left({s}−\sqrt{\mathrm{3}}{R}−\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\left({R}+{r}\right)+\mathrm{4}\left({R}^{\mathrm{2}} +{r}^{\mathrm{2}} +{Rr}\right) \\ $$$${EF}^{\mathrm{2}} ={AE}^{\mathrm{2}} +{AF}^{\mathrm{2}} −\mathrm{2}×{AE}×{AF}×\mathrm{cos}\:\mathrm{30}° \\ $$$$\left({s}−\sqrt{\mathrm{3}}{R}−\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} =\left({s}−\sqrt{\mathrm{3}}{R}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} +\left({s}−\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} −\sqrt{\mathrm{3}\left[\left({s}−\sqrt{\mathrm{3}}{R}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} \right]\left[\left({s}−\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right]} \\ $$$${s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\left({R}+{r}\right)+\mathrm{4}\left({R}^{\mathrm{2}} +{r}^{\mathrm{2}} +{Rr}\right)={s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{Rs}+\mathrm{4}{R}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{rs}+\mathrm{4}{r}^{\mathrm{2}} −\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{Rs}+\mathrm{4}{R}^{\mathrm{2}} \right)\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{rs}+\mathrm{4}{r}^{\mathrm{2}} \right)} \\ $$$${s}^{\mathrm{2}} −\mathrm{4}{Rr}=\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{Rs}+\mathrm{4}{R}^{\mathrm{2}} \right)\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{rs}+\mathrm{4}{r}^{\mathrm{2}} \right)} \\ $$$$\left({s}^{\mathrm{2}} −\mathrm{4}{Rr}\right)^{\mathrm{2}} =\mathrm{3}\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{Rs}+\mathrm{4}{R}^{\mathrm{2}} \right)\left({s}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{rs}+\mathrm{4}{r}^{\mathrm{2}} \right) \\ $$$${s}^{\mathrm{4}} −\mathrm{3}\sqrt{\mathrm{3}}\left({R}+{r}\right){s}^{\mathrm{3}} +\mathrm{2}\left(\mathrm{3}{R}^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{2}} \:+\mathrm{11}{Rr}\right){s}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}{Rr}\left({R}+{r}\right){s}+\mathrm{16}{R}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{9}\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{4}} −\mathrm{27}\left({R}+{r}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{3}{R}^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{2}} \:+\mathrm{11}{Rr}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{36}{Rr}\left({R}+{r}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{16}{R}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:{t}=\frac{{s}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{9}{t}^{\mathrm{4}} −\mathrm{27}\left({R}+{r}\right){t}^{\mathrm{3}} +\mathrm{6}\left(\mathrm{3}{R}^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{2}} +\mathrm{11}{Rr}\right){t}^{\mathrm{2}} −\mathrm{36}{Rr}\left({R}+{r}\right){t}+\mathrm{16}{R}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left[\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}\left({R}+{r}\right){t}+\mathrm{8}{Rr}\right]\left[\mathrm{3}{t}^{\mathrm{2}} −\mathrm{3}\left({R}+{r}\right){t}+\mathrm{2}{Rr}\right]=\mathrm{0} \\ $$$$\Rightarrow{t}={R}+{r}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\sqrt{\mathrm{3}\left({R}+{r}\right)^{\mathrm{2}} −\mathrm{8}{Rr}} \\ $$$$\Rightarrow{s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\sqrt{\mathrm{3}\left({R}+{r}\right)^{\mathrm{2}} −\mathrm{8}{Rr}} \\ $$$${example}: \\ $$$${R}=\mathrm{3},\:{r}=\mathrm{2} \\ $$$${s}=\sqrt{\mathrm{3}}\left(\mathrm{3}+\mathrm{2}\right)+\sqrt{\mathrm{3}×\left(\mathrm{3}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{8}×\mathrm{3}×\mathrm{2}} \\ $$$$=\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$=\mathrm{8}\sqrt{\mathrm{3}}\:\checkmark \\ $$

Answered by MJS_new last updated on 06/Jan/21

setting s=1 ∡BAD=α; 0<α<60°; k=tan α; 0<k<(√3) R=(((√3)k+1−(√(k^2 +1)))/(2(k+(√3)))) r=((2−(√(k^2 +1)))/(2(k+(√3)))) (R/r)=v I get v=((k^2 −2(√3)k−1−((√3)k−1)(√(k^2 +1)))/(k^2 −3)) ⇔ k=(((√3)(1−2v)+(v−1)(√(3v^2 −2v+3)))/(v^2 −2v−2)) from here it′s easy to calculate backwards from given R, r

$$\mathrm{setting}\:{s}=\mathrm{1} \\ $$$$\measuredangle{BAD}=\alpha;\:\mathrm{0}<\alpha<\mathrm{60}°;\:{k}=\mathrm{tan}\:\alpha;\:\mathrm{0}<{k}<\sqrt{\mathrm{3}} \\ $$$${R}=\frac{\sqrt{\mathrm{3}}{k}+\mathrm{1}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}\left({k}+\sqrt{\mathrm{3}}\right)} \\ $$$${r}=\frac{\mathrm{2}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}\left({k}+\sqrt{\mathrm{3}}\right)} \\ $$$$\frac{{R}}{{r}}={v} \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$${v}=\frac{{k}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{k}−\mathrm{1}−\left(\sqrt{\mathrm{3}}{k}−\mathrm{1}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}{{k}^{\mathrm{2}} −\mathrm{3}} \\ $$$$\Leftrightarrow \\ $$$${k}=\frac{\sqrt{\mathrm{3}}\left(\mathrm{1}−\mathrm{2}{v}\right)+\left({v}−\mathrm{1}\right)\sqrt{\mathrm{3}{v}^{\mathrm{2}} −\mathrm{2}{v}+\mathrm{3}}}{{v}^{\mathrm{2}} −\mathrm{2}{v}−\mathrm{2}} \\ $$$$\mathrm{from}\:\mathrm{here}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{backwards} \\ $$$$\mathrm{from}\:\mathrm{given}\:{R},\:{r} \\ $$

Commented by mr W last updated on 06/Jan/21

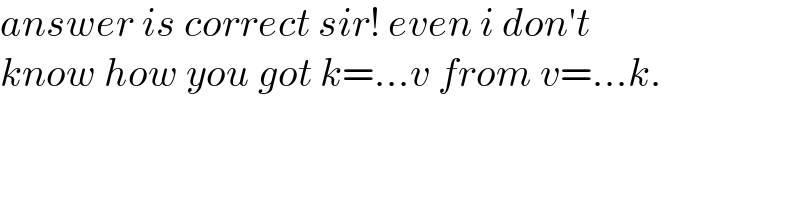
$${answer}\:{is}\:{correct}\:{sir}!\:{even}\:{i}\:{don}'{t} \\ $$$${know}\:{how}\:{you}\:{got}\:{k}=…{v}\:{from}\:{v}=…{k}. \\ $$

Commented by MJS_new last updated on 06/Jan/21

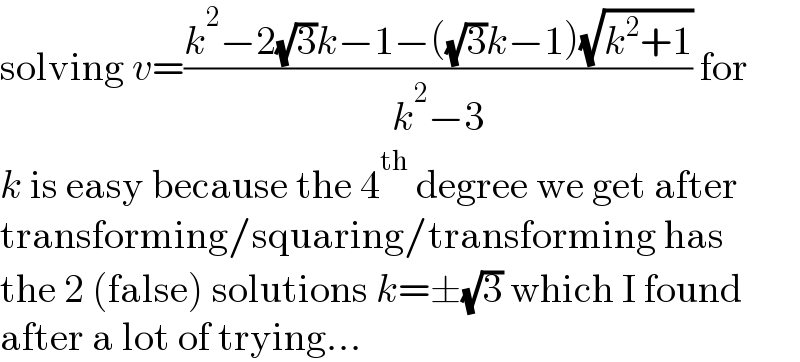
solving v=((k^2 −2(√3)k−1−((√3)k−1)(√(k^2 +1)))/(k^2 −3)) for k is easy because the 4^(th) degree we get after transforming/squaring/transforming has the 2 (false) solutions k=±(√3) which I found after a lot of trying...

$$\mathrm{solving}\:{v}=\frac{{k}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{k}−\mathrm{1}−\left(\sqrt{\mathrm{3}}{k}−\mathrm{1}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}{{k}^{\mathrm{2}} −\mathrm{3}}\:\mathrm{for} \\ $$$${k}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{because}\:\mathrm{the}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{we}\:\mathrm{get}\:\mathrm{after} \\ $$$$\mathrm{transforming}/\mathrm{squaring}/\mathrm{transforming}\:\mathrm{has} \\ $$$$\mathrm{the}\:\mathrm{2}\:\left(\mathrm{false}\right)\:\mathrm{solutions}\:{k}=\pm\sqrt{\mathrm{3}}\:\mathrm{which}\:\mathrm{I}\:\mathrm{found} \\ $$$$\mathrm{after}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{trying}… \\ $$

Commented by mr W last updated on 06/Jan/21

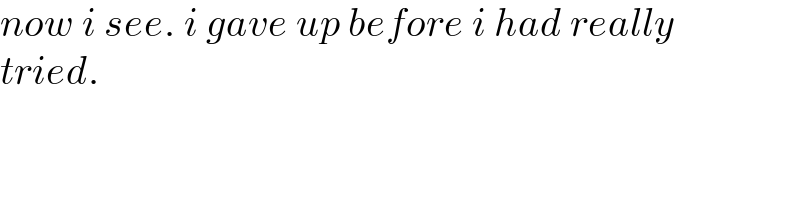
$${now}\:{i}\:{see}.\:{i}\:{gave}\:{up}\:{before}\:{i}\:{had}\:{really} \\ $$$${tried}. \\ $$

Answered by ajfour last updated on 07/Jan/21

Commented by ajfour last updated on 07/Jan/21

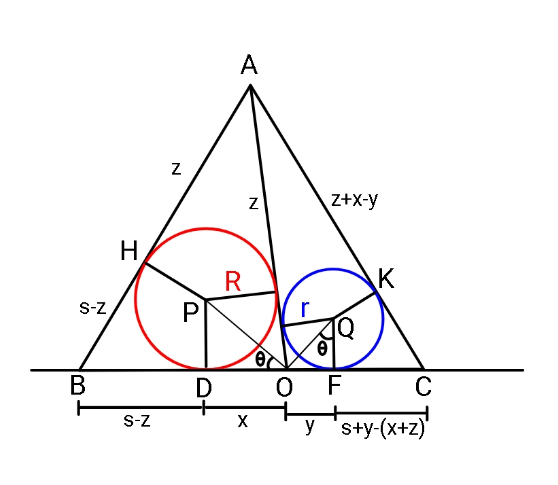
tan θ=m x=(R/m) , y=mr s−z=R(√3) ⇒ z=s−R(√3) ..(i) s+y−(x+z)=r(√3) BD+DO+OF+FC = s R(√3)+(R/m)+mr+r(√3) = s ...(ii) ((PH)/(AH))=(R/z)=tan (60°−θ) ...(iii) (r/(z+x−y))=tan (θ−30°) ....(iv) equating z+x−y from (iii), (iv): (R/(tan (60−θ)))+(R/m)−mr=(r/(tan (θ−30))) ((R(1+m(√3)))/( (√3)−m))+(R/m)−mr=((r(m+(√3)))/(m(√3)−1)) ⇒ ((R[m+m^2 (√3)+(√3)−m])/( m((√3)−m)))=((r[m^2 (√3)+(√3)])/(m(√3)−1)) ⇒ (R/(m((√3)−m)))=(r/(m(√3)−1)) ⇒ mR(√3)−R=mr(√3)−m^2 r rm^2 +m(R−r)(√3)−R=0 m=−(((R−r)(√3))/(2r))+(√(((3(R−r)^2 )/(4r^2 ))+(R/r))) (R/m^2 )−(((R−r)(√3))/m)−r=0 (1/m)=(((R−r)(√3))/(2R))+(√(((3(R−r)^2 )/(4R^2 ))+(r/R))) substituting in (ii) s=(√3)(R+r)+(R/m)+mr s=(√3)(R+r)+(((R−r)(√3))/2) +(√(((3(R−r)^2 )/4)+rR)) −(((R−r)(√3))/2)+(√(((3(R−r)^2 )/4)+rR)) ⇒ s=(√3)(R+r)+(√(3(R−r)^2 +4rR))

$$\mathrm{tan}\:\theta={m} \\ $$$${x}=\frac{{R}}{{m}}\:,\:\:\:{y}={mr} \\ $$$${s}−{z}={R}\sqrt{\mathrm{3}}\:\:\:\:\:\Rightarrow\:\:{z}={s}−{R}\sqrt{\mathrm{3}}\:\:..\left({i}\right) \\ $$$${s}+{y}−\left({x}+{z}\right)={r}\sqrt{\mathrm{3}} \\ $$$${BD}+{DO}+{OF}+{FC}\:=\:{s} \\ $$$${R}\sqrt{\mathrm{3}}+\frac{{R}}{{m}}+{mr}+{r}\sqrt{\mathrm{3}}\:=\:{s}\:\:\:…\left({ii}\right) \\ $$$$\frac{{PH}}{{AH}}=\frac{{R}}{{z}}=\mathrm{tan}\:\left(\mathrm{60}°−\theta\right)\:\:\:\:\:…\left({iii}\right) \\ $$$$\frac{{r}}{{z}+{x}−{y}}=\mathrm{tan}\:\left(\theta−\mathrm{30}°\right)\:\:\:\:\:….\left({iv}\right) \\ $$$${equating}\:{z}+{x}−{y}\:{from}\:\left({iii}\right),\:\left({iv}\right): \\ $$$$\:\:\frac{{R}}{\mathrm{tan}\:\left(\mathrm{60}−\theta\right)}+\frac{{R}}{{m}}−{mr}=\frac{{r}}{\mathrm{tan}\:\left(\theta−\mathrm{30}\right)} \\ $$$$\frac{{R}\left(\mathrm{1}+{m}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}−{m}}+\frac{{R}}{{m}}−{mr}=\frac{{r}\left({m}+\sqrt{\mathrm{3}}\right)}{{m}\sqrt{\mathrm{3}}−\mathrm{1}} \\ $$$$\Rightarrow\:\: \\ $$$$\frac{{R}\left[{m}+{m}^{\mathrm{2}} \sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}−{m}\right]}{\:{m}\left(\sqrt{\mathrm{3}}−{m}\right)}=\frac{{r}\left[{m}^{\mathrm{2}} \sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}\right]}{{m}\sqrt{\mathrm{3}}−\mathrm{1}} \\ $$$$\Rightarrow\:\:\frac{{R}}{{m}\left(\sqrt{\mathrm{3}}−{m}\right)}=\frac{{r}}{{m}\sqrt{\mathrm{3}}−\mathrm{1}} \\ $$$$\Rightarrow\:\:{mR}\sqrt{\mathrm{3}}−{R}={mr}\sqrt{\mathrm{3}}−{m}^{\mathrm{2}} {r} \\ $$$$\:\:{rm}^{\mathrm{2}} +{m}\left({R}−{r}\right)\sqrt{\mathrm{3}}−{R}=\mathrm{0} \\ $$$$\:{m}=−\frac{\left({R}−{r}\right)\sqrt{\mathrm{3}}}{\mathrm{2}{r}}+\sqrt{\frac{\mathrm{3}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }+\frac{{R}}{{r}}} \\ $$$$\:\:\frac{{R}}{{m}^{\mathrm{2}} }−\frac{\left({R}−{r}\right)\sqrt{\mathrm{3}}}{{m}}−{r}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{m}}=\frac{\left({R}−{r}\right)\sqrt{\mathrm{3}}}{\mathrm{2}{R}}+\sqrt{\frac{\mathrm{3}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }+\frac{{r}}{{R}}} \\ $$$${substituting}\:{in}\:\left({ii}\right) \\ $$$$\:\:{s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\frac{{R}}{{m}}+{mr} \\ $$$${s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\frac{\left({R}−{r}\right)\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\:+\sqrt{\frac{\mathrm{3}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}}+{rR}} \\ $$$$\:\:\:\:−\frac{\left({R}−{r}\right)\sqrt{\mathrm{3}}}{\mathrm{2}}+\sqrt{\frac{\mathrm{3}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}}+{rR}} \\ $$$$\Rightarrow \\ $$$$\:{s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\sqrt{\mathrm{3}\left({R}−{r}\right)^{\mathrm{2}} +\mathrm{4}{rR}} \\ $$

Commented by mr W last updated on 07/Jan/21