Question Number 128458 by SLVR last updated on 07/Jan/21

Commented by BHOOPENDRA last updated on 07/Jan/21
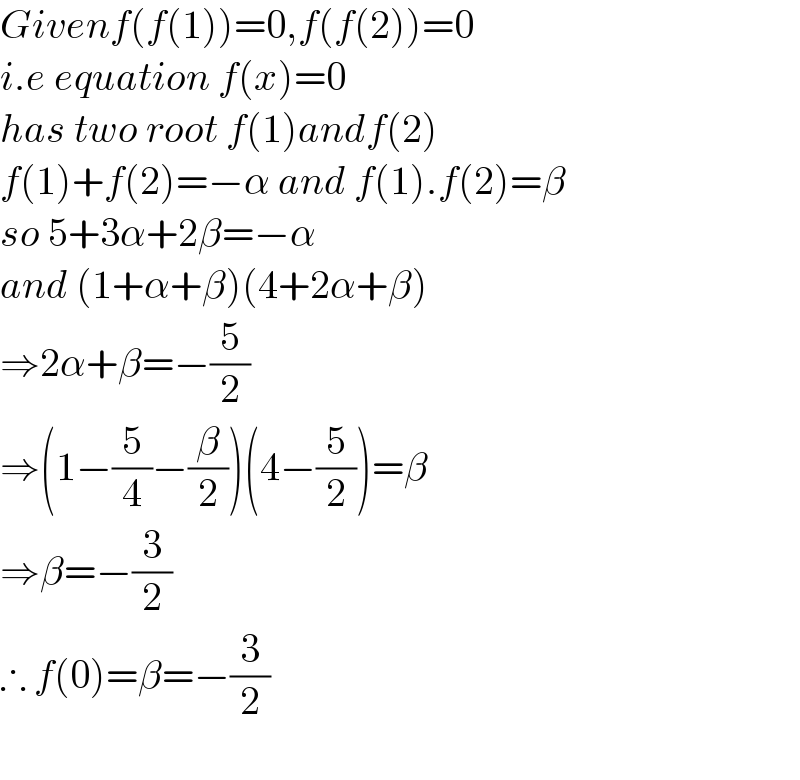
$${Givenf}\left({f}\left(\mathrm{1}\right)\right)=\mathrm{0},{f}\left({f}\left(\mathrm{2}\right)\right)=\mathrm{0} \\ $$$${i}.{e}\:{equation}\:{f}\left({x}\right)=\mathrm{0} \\ $$$${has}\:{two}\:{root}\:{f}\left(\mathrm{1}\right){andf}\left(\mathrm{2}\right) \\ $$$${f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)=−\alpha\:{and}\:{f}\left(\mathrm{1}\right).{f}\left(\mathrm{2}\right)=\beta \\ $$$${so}\:\mathrm{5}+\mathrm{3}\alpha+\mathrm{2}\beta=−\alpha \\ $$$${and}\:\left(\mathrm{1}+\alpha+\beta\right)\left(\mathrm{4}+\mathrm{2}\alpha+\beta\right) \\ $$$$\Rightarrow\mathrm{2}\alpha+\beta=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{1}−\frac{\mathrm{5}}{\mathrm{4}}−\frac{\beta}{\mathrm{2}}\right)\left(\mathrm{4}−\frac{\mathrm{5}}{\mathrm{2}}\right)=\beta \\ $$$$\Rightarrow\beta=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\therefore\:{f}\left(\mathrm{0}\right)=\beta=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$
