Question Number 128518 by shaker last updated on 08/Jan/21

Commented by bramlexs22 last updated on 08/Jan/21
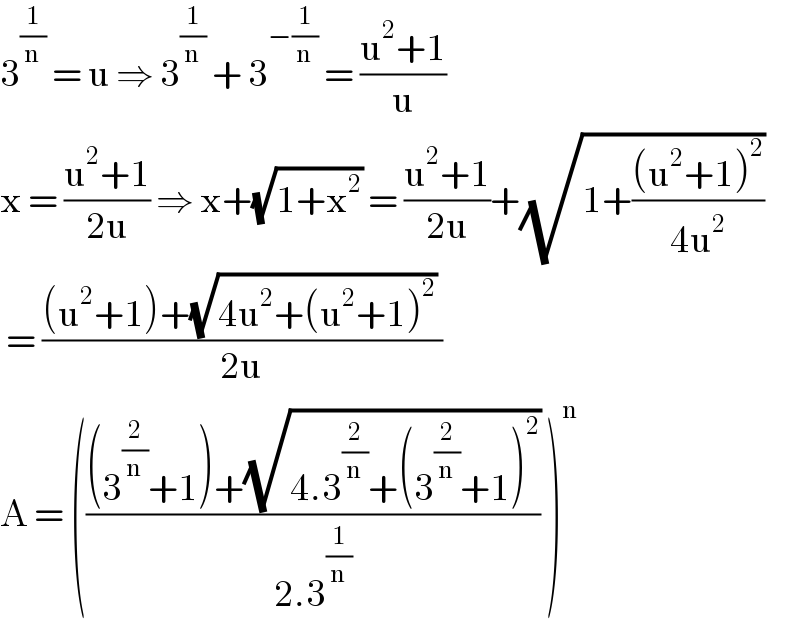
$$\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\:\mathrm{u}\:\Rightarrow\:\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{n}}} \:+\:\mathrm{3}^{−\frac{\mathrm{1}}{\mathrm{n}}} \:=\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{u}} \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2u}}\:\Rightarrow\:\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2u}}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4u}^{\mathrm{2}} }} \\ $$$$\:=\:\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)+\sqrt{\mathrm{4u}^{\mathrm{2}} +\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:}{\mathrm{2u}} \\ $$$$\mathrm{A}\:=\:\left(\frac{\left(\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{n}}} +\mathrm{1}\right)+\sqrt{\mathrm{4}.\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{n}}} +\left(\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{n}}} +\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}.\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{n}}} }\:\right)^{\mathrm{n}} \\ $$
Commented by bramlexs22 last updated on 08/Jan/21
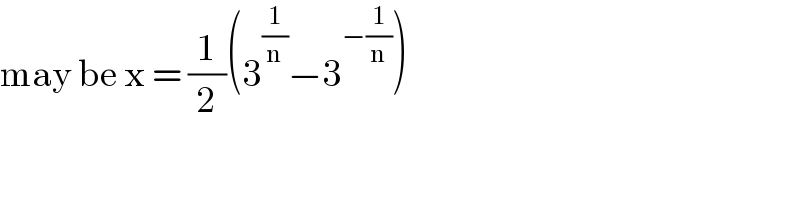
$$\mathrm{may}\:\mathrm{be}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{n}}} −\mathrm{3}^{−\frac{\mathrm{1}}{\mathrm{n}}} \right) \\ $$
Answered by MJS_new last updated on 08/Jan/21
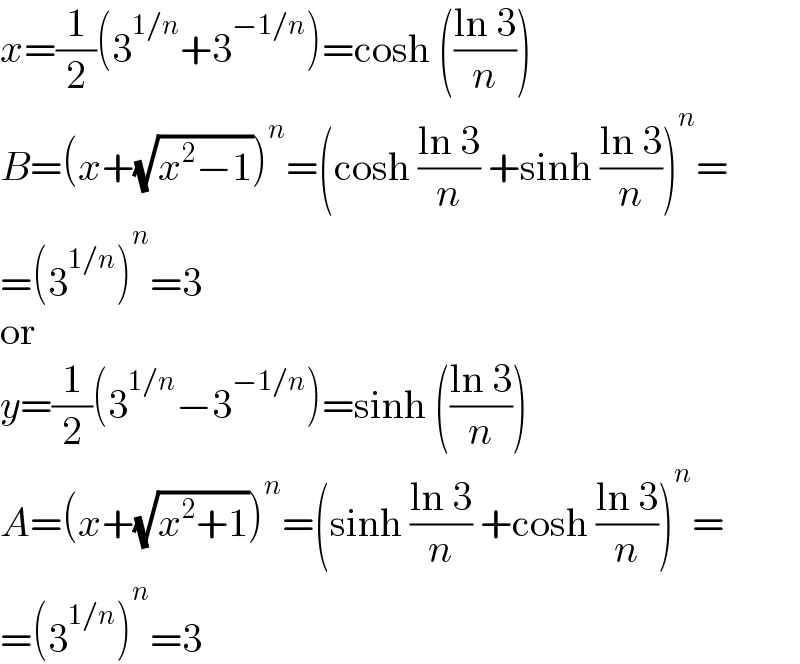
$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\mathrm{1}/{n}} +\mathrm{3}^{−\mathrm{1}/{n}} \right)=\mathrm{cosh}\:\left(\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\right) \\ $$$${B}=\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)^{{n}} =\left(\mathrm{cosh}\:\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\:+\mathrm{sinh}\:\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\right)^{{n}} = \\ $$$$=\left(\mathrm{3}^{\mathrm{1}/{n}} \right)^{{n}} =\mathrm{3} \\ $$$$\mathrm{or} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\mathrm{1}/{n}} −\mathrm{3}^{−\mathrm{1}/{n}} \right)=\mathrm{sinh}\:\left(\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\right) \\ $$$${A}=\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{{n}} =\left(\mathrm{sinh}\:\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\:+\mathrm{cosh}\:\frac{\mathrm{ln}\:\mathrm{3}}{{n}}\right)^{{n}} = \\ $$$$=\left(\mathrm{3}^{\mathrm{1}/{n}} \right)^{{n}} =\mathrm{3} \\ $$
Commented by bramlexs22 last updated on 08/Jan/21

$$\mathrm{waw}…\mathrm{amazing} \\ $$
