Question-128529

Question Number 128529 by bramlexs22 last updated on 08/Jan/21

Commented by liberty last updated on 08/Jan/21

considering \frac{d}{dx} (\frac{u}{v}) = \frac{u^{'} v - {uv}^{'}}{v^{2}}

obvious v = 2 + 3 \cos x and 3 + 2 \cos x = u^{'} (2 + 3 \cos x) - u (- 3 \sin x)

\Rightarrow 2 \cos x + 3 = {2 u}^{'} + {3 u}^{'} \cos x + 3 u \sin x

check u = \sin x \Rightarrow u^{'} (2 + 3 cosx) + 3 u \sin x =

2 \cos x + {3 \cos}^{2} x + {3 \sin}^{2} x = 2 \cos x + 3 (valid)

therefore \int \frac{3 + 2 \cos x}{{(2 + 3 \cos x)}^{2}} dx = \frac{\sin x}{2 + 3 \cos x}

Commented by SLVR last updated on 08/Jan/21

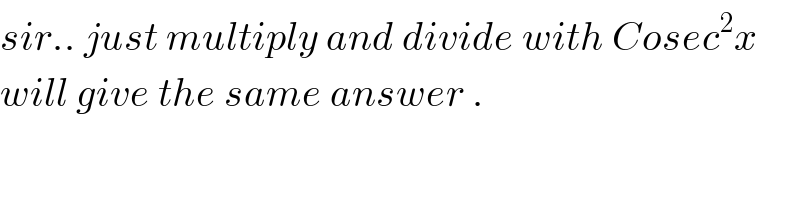
s i r . . j u s t m u l t i p l y a n d d i v i d e w i t h {C o s e c}^{2} x

w i l l g i v e t h e s a m e a n s w e r .

Answered by SLVR last updated on 08/Jan/21

Commented by bramlexs22 last updated on 08/Jan/21

what ?

Commented by SLVR last updated on 08/Jan/21

i h o p e a r e a g r e e d w i t h t h e s o l u t i o n

Commented by john_santu last updated on 08/Jan/21

what your solution ?

Commented by SLVR last updated on 09/Jan/21

Commented by SLVR last updated on 09/Jan/21

s o r r y \dots i d i d n o t o b s e r v e d u p l o a d i n g p a r t

Facebook Tweet Pin