Question Number 128646 by Algoritm last updated on 09/Jan/21
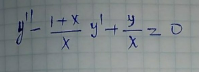
Answered by Olaf last updated on 09/Jan/21
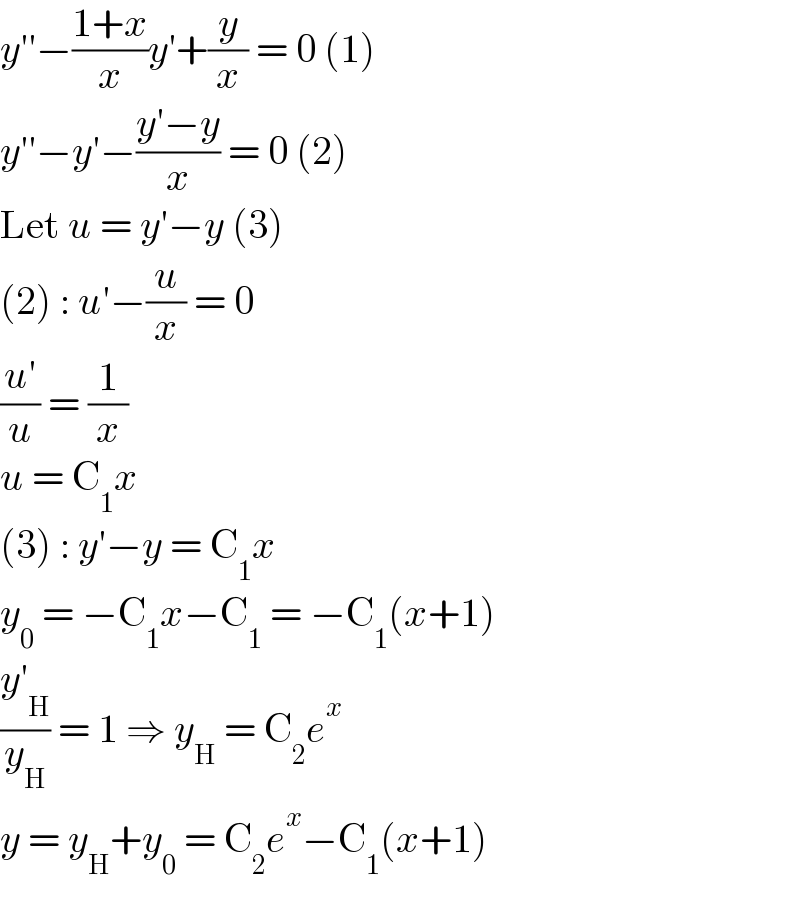
$${y}''−\frac{\mathrm{1}+{x}}{{x}}{y}'+\frac{{y}}{{x}}\:=\:\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$${y}''−{y}'−\frac{{y}'−{y}}{{x}}\:=\:\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{Let}\:{u}\:=\:{y}'−{y}\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\::\:{u}'−\frac{{u}}{{x}}\:=\:\mathrm{0} \\ $$$$\frac{{u}'}{{u}}\:=\:\frac{\mathrm{1}}{{x}} \\ $$$${u}\:=\:\mathrm{C}_{\mathrm{1}} {x} \\ $$$$\left(\mathrm{3}\right)\::\:{y}'−{y}\:=\:\mathrm{C}_{\mathrm{1}} {x} \\ $$$${y}_{\mathrm{0}} \:=\:−\mathrm{C}_{\mathrm{1}} {x}−\mathrm{C}_{\mathrm{1}} \:=\:−\mathrm{C}_{\mathrm{1}} \left({x}+\mathrm{1}\right) \\ $$$$\frac{{y}'_{\mathrm{H}} }{{y}_{\mathrm{H}} }\:=\:\mathrm{1}\:\Rightarrow\:{y}_{\mathrm{H}} \:=\:\mathrm{C}_{\mathrm{2}} {e}^{{x}} \\ $$$${y}\:=\:{y}_{\mathrm{H}} +{y}_{\mathrm{0}} \:=\:\mathrm{C}_{\mathrm{2}} {e}^{{x}} −\mathrm{C}_{\mathrm{1}} \left({x}+\mathrm{1}\right) \\ $$
