Question Number 128660 by help last updated on 09/Jan/21
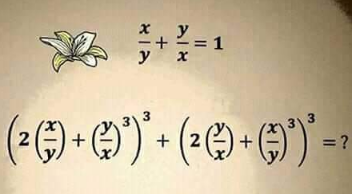
Commented by harckinwunmy last updated on 09/Jan/21

$${ff} \\ $$
Answered by liberty last updated on 09/Jan/21
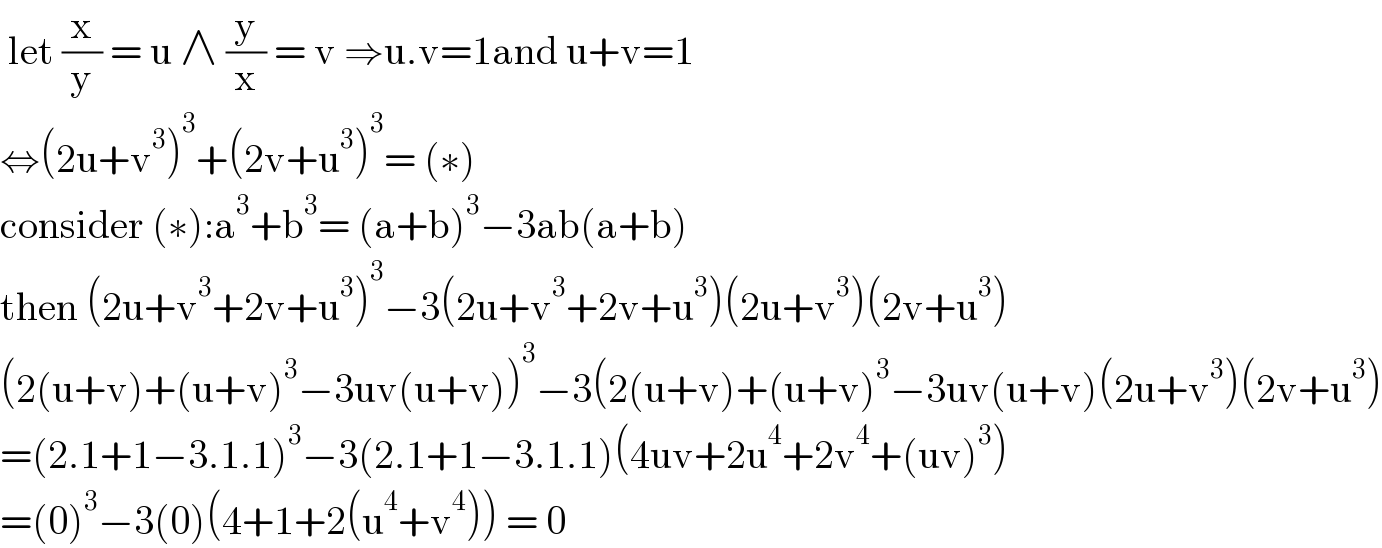
$$\:\mathrm{let}\:\frac{\mathrm{x}}{\mathrm{y}}\:=\:\mathrm{u}\:\wedge\:\frac{\mathrm{y}}{\mathrm{x}}\:=\:\mathrm{v}\:\Rightarrow\mathrm{u}.\mathrm{v}=\mathrm{1and}\:\mathrm{u}+\mathrm{v}=\mathrm{1} \\ $$$$\Leftrightarrow\left(\mathrm{2u}+\mathrm{v}^{\mathrm{3}} \right)^{\mathrm{3}} +\left(\mathrm{2v}+\mathrm{u}^{\mathrm{3}} \right)^{\mathrm{3}} =\:\left(\ast\right) \\ $$$$\mathrm{consider}\:\left(\ast\right):\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{3}} −\mathrm{3ab}\left(\mathrm{a}+\mathrm{b}\right) \\ $$$$\mathrm{then}\:\left(\mathrm{2u}+\mathrm{v}^{\mathrm{3}} +\mathrm{2v}+\mathrm{u}^{\mathrm{3}} \right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{2u}+\mathrm{v}^{\mathrm{3}} +\mathrm{2v}+\mathrm{u}^{\mathrm{3}} \right)\left(\mathrm{2u}+\mathrm{v}^{\mathrm{3}} \right)\left(\mathrm{2v}+\mathrm{u}^{\mathrm{3}} \right) \\ $$$$\left(\mathrm{2}\left(\mathrm{u}+\mathrm{v}\right)+\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{3}} −\mathrm{3uv}\left(\mathrm{u}+\mathrm{v}\right)\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{2}\left(\mathrm{u}+\mathrm{v}\right)+\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{3}} −\mathrm{3uv}\left(\mathrm{u}+\mathrm{v}\right)\left(\mathrm{2u}+\mathrm{v}^{\mathrm{3}} \right)\left(\mathrm{2v}+\mathrm{u}^{\mathrm{3}} \right)\right. \\ $$$$=\left(\mathrm{2}.\mathrm{1}+\mathrm{1}−\mathrm{3}.\mathrm{1}.\mathrm{1}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{2}.\mathrm{1}+\mathrm{1}−\mathrm{3}.\mathrm{1}.\mathrm{1}\right)\left(\mathrm{4uv}+\mathrm{2u}^{\mathrm{4}} +\mathrm{2v}^{\mathrm{4}} +\left(\mathrm{uv}\right)^{\mathrm{3}} \right) \\ $$$$=\left(\mathrm{0}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{0}\right)\left(\mathrm{4}+\mathrm{1}+\mathrm{2}\left(\mathrm{u}^{\mathrm{4}} +\mathrm{v}^{\mathrm{4}} \right)\right)\:=\:\mathrm{0} \\ $$
Commented by bemath last updated on 09/Jan/21
��♂��♀��♂��♀��♂������
