Question Number 128698 by I want to learn more last updated on 09/Jan/21
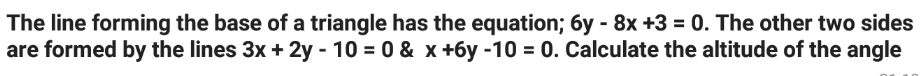
Commented by I want to learn more last updated on 09/Jan/21
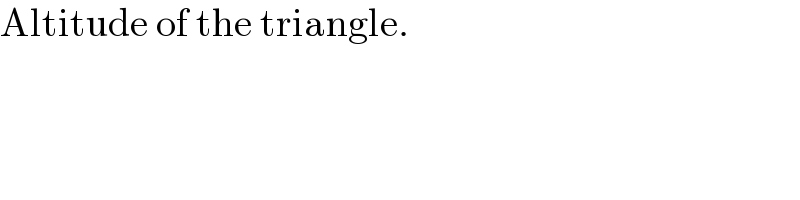
$$\mathrm{Altitude}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}. \\ $$
Commented by liberty last updated on 09/Jan/21
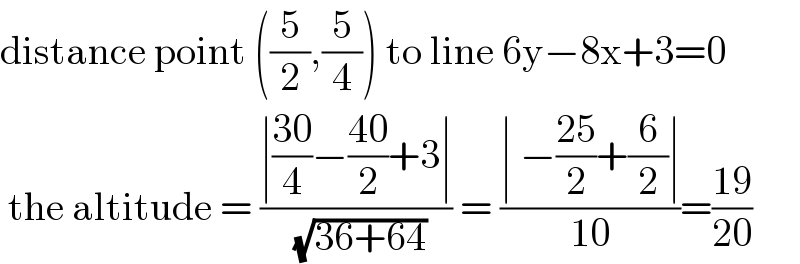
$$\mathrm{distance}\:\mathrm{point}\:\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{4}}\right)\:\mathrm{to}\:\mathrm{line}\:\mathrm{6y}−\mathrm{8x}+\mathrm{3}=\mathrm{0} \\ $$$$\:\mathrm{the}\:\mathrm{altitude}\:=\:\frac{\mid\frac{\mathrm{30}}{\mathrm{4}}−\frac{\mathrm{40}}{\mathrm{2}}+\mathrm{3}\mid}{\:\sqrt{\mathrm{36}+\mathrm{64}}}\:=\:\frac{\mid\:−\frac{\mathrm{25}}{\mathrm{2}}+\frac{\mathrm{6}}{\mathrm{2}}\mid}{\mathrm{10}}=\frac{\mathrm{19}}{\mathrm{20}} \\ $$
Commented by I want to learn more last updated on 10/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 09/Jan/21

$${intersection}\:{of}\: \\ $$$$\mathrm{3}{x}+\mathrm{2}{y}−\mathrm{10}=\mathrm{0}\:{and} \\ $$$${x}+\mathrm{6}{y}−\mathrm{10}=\mathrm{0} \\ $$$$\Rightarrow{y}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${distance}\:{from}\:\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{4}}\right)\:{to}\:{base} \\ $$$$\mathrm{6}{y}−\mathrm{8}{x}+\mathrm{3}=\mathrm{0} \\ $$$${is} \\ $$$${h}=\frac{\mid−\mathrm{8}×\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{6}×\frac{\mathrm{5}}{\mathrm{4}}+\mathrm{3}\mid}{\:\sqrt{\left(−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }}=\frac{\mathrm{19}}{\mathrm{20}} \\ $$$${which}\:{is}\:{also}\:{the}\:{altitude}. \\ $$
Commented by I want to learn more last updated on 10/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
