Question Number 128830 by bemath last updated on 10/Jan/21

Answered by liberty last updated on 10/Jan/21
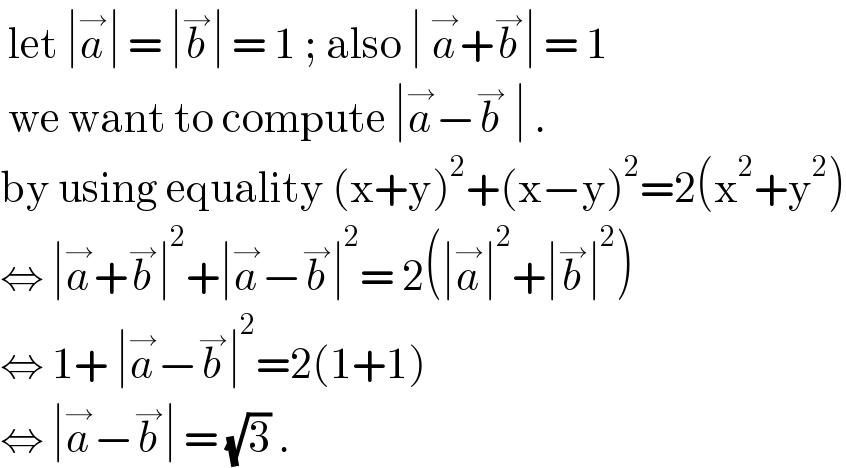
$$\:\mathrm{let}\:\mid\overset{\rightarrow} {{a}}\mid\:=\:\mid\overset{\rightarrow} {{b}}\mid\:=\:\mathrm{1}\:;\:\mathrm{also}\:\mid\:\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\mid\:=\:\mathrm{1}\: \\ $$$$\:\mathrm{we}\:\mathrm{want}\:\mathrm{to}\:\mathrm{compute}\:\mid\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}\:\mid\:. \\ $$$$\mathrm{by}\:\mathrm{using}\:\mathrm{equality}\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} +\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\:\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} =\:\mathrm{2}\left(\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\:\mathrm{1}+\:\mid\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}+\mathrm{1}\right)\: \\ $$$$\Leftrightarrow\:\mid\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}\mid\:=\:\sqrt{\mathrm{3}}\:. \\ $$
Answered by mr W last updated on 10/Jan/21

Commented by mr W last updated on 10/Jan/21

$$\mid{a}\mid=\mid{b}\mid=\mathrm{1} \\ $$$$\mid{a}+{b}\mid=\mathrm{1} \\ $$$$\Rightarrow\mid{a}−{b}\mid=\sqrt{\mathrm{3}} \\ $$
