Question Number 128892 by n0y0n last updated on 11/Jan/21

Commented by mr W last updated on 11/Jan/21

$${r}={distance}\:{from}\:{pedal}\:{point}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:{to}\:{a}\:{point}\:{C}\left({x},{y}\right)\:{on}\:{a}\:{curve} \\ $$$${p}={distance}\:{from}\:{pedal}\:{point}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:{to}\:{the}\:{tangent}\:{of}\:{the}\:{curve}\:{at}\:{the} \\ $$$$\:\:\:\:\:\:\:{point}\:{C}\left({x},{y}\right). \\ $$$${the}\:{equation}\:{which}\:{expresses}\:{the} \\ $$$${relation}\:{between}\:{r}\:{and}\:{p}\:{is}\:{called} \\ $$$${the}\:{pedal}\:{equation}\:{of}\:{the}\:{curve}. \\ $$
Commented by bemath last updated on 11/Jan/21
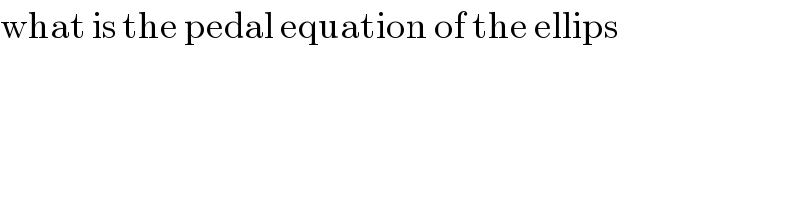
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{pedal}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ellips} \\ $$
Commented by mr W last updated on 11/Jan/21

$${for}\:{ellipse}\:{it}\:{is} \\ $$$${r}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{p}^{\mathrm{2}} }={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$
Answered by BHOOPENDRA last updated on 11/Jan/21

$${the}\:{equation}\:{of}\:{the}\:{tangent}\:{is}\: \\ $$$${given} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}−−−−\left(\mathrm{1}\right) \\ $$$${it}\:{can}\:{be}\:{written}\:{as}\: \\ $$$$\Rightarrow\frac{{xX}}{{a}^{\mathrm{2}} }+\frac{{yY}}{{b}^{\mathrm{2}} }=\mathrm{1}−−−−−\left(\mathrm{2}\right) \\ $$$${Now}\:{we}\:{can}\:{compare}\:{AX}+{By}+{c}=\mathrm{0} \\ $$$${with}\:{perpendicular}\:{distance}\:{formula} \\ $$$$\left(\mathrm{0},\mathrm{0}\right) \\ $$$${P}=−\mid\frac{{c}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}\:\mid{whereA}^{\mathrm{2}} =\frac{{x}}{{a}^{\mathrm{4}} },{B}^{\mathrm{2}} =\frac{{y}}{{b}^{\mathrm{4}} } \\ $$$${now}\:{r}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }=\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{4}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{4}} }−−−−−\left(\mathrm{3}\right) \\ $$$${now}\:{after}\:{simlification} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\frac{{r}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }−−−−−\left(\mathrm{4}\right) \\ $$$${similarly}\: \\ $$$$\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }−−−−−−\left(\mathrm{5}\right) \\ $$$${now}\:{put}\:{value}\:{in}\:{equation}\:\left(\mathrm{3}\right) \\ $$$${we}\:{will}\:{get}\: \\ $$$$\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{p}^{\mathrm{2}} }={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${And}\:{this}\:{will}\:{be}\:{your}\:{pedal}\:{equation} \\ $$
