Question Number 128893 by BHOOPENDRA last updated on 11/Jan/21

Answered by Dwaipayan Shikari last updated on 11/Jan/21
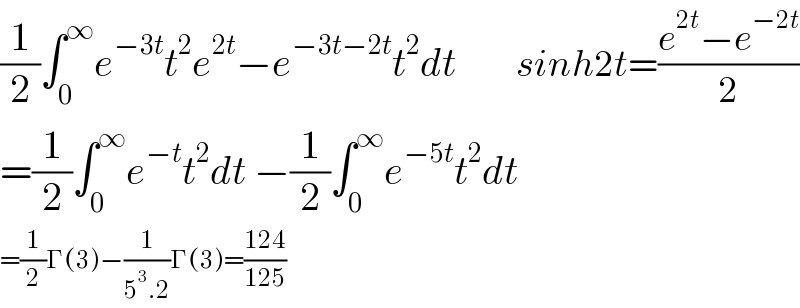
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{t}} {t}^{\mathrm{2}} {e}^{\mathrm{2}{t}} −{e}^{−\mathrm{3}{t}−\mathrm{2}{t}} {t}^{\mathrm{2}} {dt}\:\:\:\:\:\:\:\:\:\:{sinh}\mathrm{2}{t}=\frac{{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{\mathrm{2}} {dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{5}{t}} {t}^{\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} .\mathrm{2}}\Gamma\left(\mathrm{3}\right)=\frac{\mathrm{124}}{\mathrm{125}} \\ $$
