Question Number 128910 by shaker last updated on 11/Jan/21

Answered by bramlexs22 last updated on 11/Jan/21
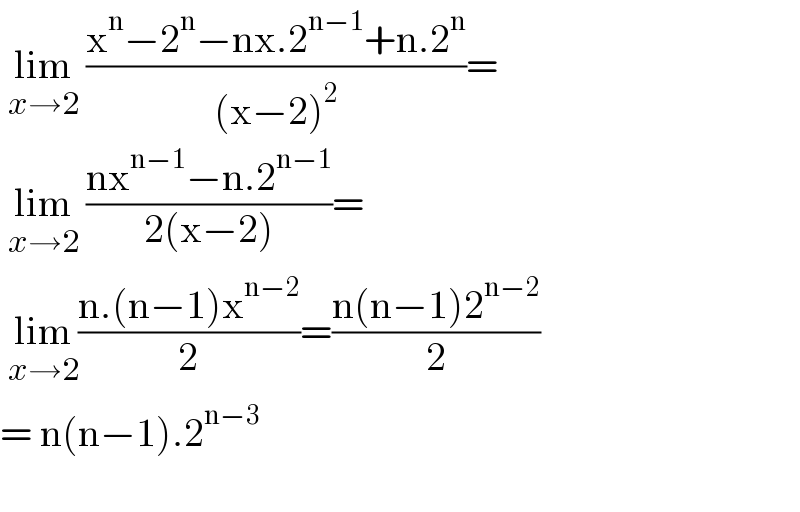
$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{2}^{\mathrm{n}} −\mathrm{nx}.\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{n}.\mathrm{2}^{\mathrm{n}} }{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} −\mathrm{n}.\mathrm{2}^{\mathrm{n}−\mathrm{1}} }{\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)}= \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{n}.\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}} \\ $$$$=\:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right).\mathrm{2}^{\mathrm{n}−\mathrm{3}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 11/Jan/21

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{2}^{\mathrm{n}} −\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}−\mathrm{2}\right)}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}−\mathrm{2}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{t}\right)=\frac{\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{n}} −\mathrm{2}^{\mathrm{n}} −\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \:\mathrm{2}^{\mathrm{n}−\mathrm{k}} −\mathrm{2}^{\mathrm{n}} −\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}^{\mathrm{n}} \:+\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \mathrm{t}\:+\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \:\mathrm{2}^{\mathrm{n}−\mathrm{k}} −\mathrm{2}^{\mathrm{n}} −\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}−\mathrm{2}} \:\mathrm{2}^{\mathrm{n}−\mathrm{k}} \:\:\left(\mathrm{k}−\mathrm{2}=\mathrm{i}\right) \\ $$$$=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}−\mathrm{2}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{i}+\mathrm{2}} \:\mathrm{t}^{\mathrm{i}} \:\mathrm{2}^{\mathrm{n}−\mathrm{i}−\mathrm{2}} \:\:\:\:\:\:\left(\mathrm{x}\rightarrow\mathrm{2}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$=\mathrm{C}_{\mathrm{n}} ^{\mathrm{2}} \:\mathrm{2}^{\mathrm{n}−\mathrm{2}} \:+\mathrm{C}_{\mathrm{n}} ^{\mathrm{3}} \:\mathrm{t}\:\mathrm{2}^{\mathrm{n}−\mathrm{3}} \:+…..\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=\mathrm{2}^{\mathrm{n}−\mathrm{2}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{2}} \:\:=\mathrm{2}^{\mathrm{n}−\mathrm{2}} ×\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{2}\right)!\mathrm{2}!} \\ $$$$=\mathrm{2}^{\mathrm{n}−\mathrm{2}} ×\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}\:=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{n}−\mathrm{3}} \\ $$
