Question-128932

Question Number 128932 by Koyoooo last updated on 11/Jan/21

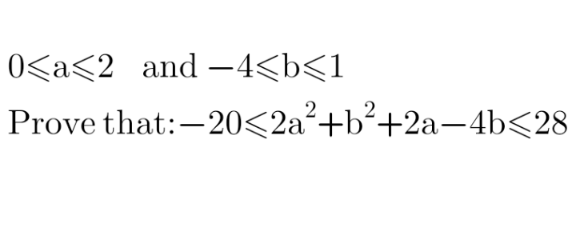
Commented by mr W last updated on 11/Jan/21

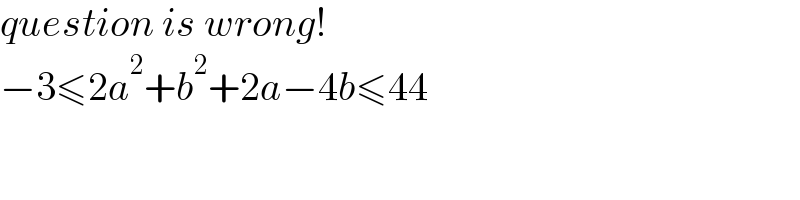
question is wrong! −3≤2a^2 +b^2 +2a−4b≤44

$${question}\:{is}\:{wrong}! \\ $$$$−\mathrm{3}\leqslant\mathrm{2}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{4}{b}\leqslant\mathrm{44} \\ $$

Commented by liberty last updated on 12/Jan/21

$$\mathrm{yes}\:\mathrm{question}\:\mathrm{wrong} \\ $$$$ \\ $$

Commented by liberty last updated on 12/Jan/21

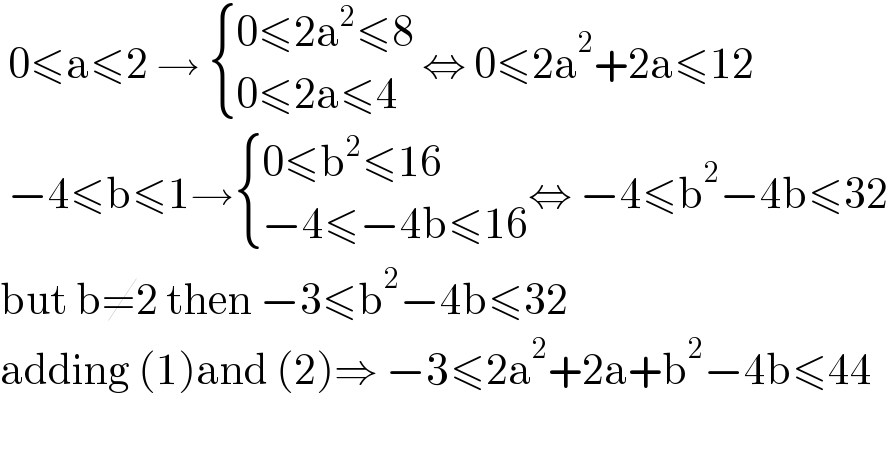
0≤a≤2 → { ((0≤2a^2 ≤8)),((0≤2a≤4)) :} ⇔ 0≤2a^2 +2a≤12 −4≤b≤1→ { ((0≤b^2 ≤16)),((−4≤−4b≤16)) :}⇔ −4≤b^2 −4b≤32 but b≠2 then −3≤b^2 −4b≤32 adding (1)and (2)⇒ −3≤2a^2 +2a+b^2 −4b≤44

$$\:\mathrm{0}\leqslant\mathrm{a}\leqslant\mathrm{2}\:\rightarrow\:\begin{cases}{\mathrm{0}\leqslant\mathrm{2a}^{\mathrm{2}} \leqslant\mathrm{8}}\\{\mathrm{0}\leqslant\mathrm{2a}\leqslant\mathrm{4}}\end{cases}\:\Leftrightarrow\:\mathrm{0}\leqslant\mathrm{2a}^{\mathrm{2}} +\mathrm{2a}\leqslant\mathrm{12} \\ $$$$\:−\mathrm{4}\leqslant\mathrm{b}\leqslant\mathrm{1}\rightarrow\begin{cases}{\mathrm{0}\leqslant\mathrm{b}^{\mathrm{2}} \leqslant\mathrm{16}}\\{−\mathrm{4}\leqslant−\mathrm{4b}\leqslant\mathrm{16}}\end{cases}\Leftrightarrow\:−\mathrm{4}\leqslant\mathrm{b}^{\mathrm{2}} −\mathrm{4b}\leqslant\mathrm{32}\: \\ $$$$\mathrm{but}\:\mathrm{b}\neq\mathrm{2}\:\mathrm{then}\:−\mathrm{3}\leqslant\mathrm{b}^{\mathrm{2}} −\mathrm{4b}\leqslant\mathrm{32} \\ $$$$\mathrm{adding}\:\left(\mathrm{1}\right)\mathrm{and}\:\left(\mathrm{2}\right)\Rightarrow\:−\mathrm{3}\leqslant\mathrm{2a}^{\mathrm{2}} +\mathrm{2a}+\mathrm{b}^{\mathrm{2}} −\mathrm{4b}\leqslant\mathrm{44}\: \\ $$$$ \\ $$

Answered by mr W last updated on 11/Jan/21

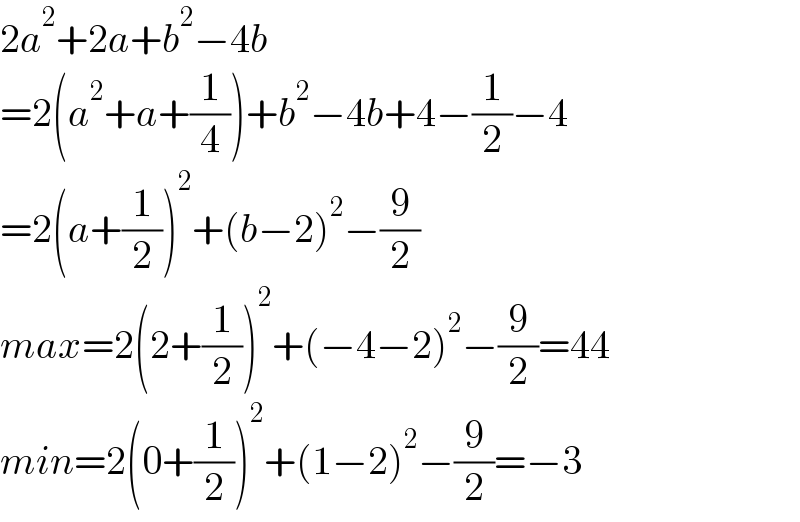
2a^2 +2a+b^2 −4b =2(a^2 +a+(1/4))+b^2 −4b+4−(1/2)−4 =2(a+(1/2))^2 +(b−2)^2 −(9/2) max=2(2+(1/2))^2 +(−4−2)^2 −(9/2)=44 min=2(0+(1/2))^2 +(1−2)^2 −(9/2)=−3

$$\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}+{b}^{\mathrm{2}} −\mathrm{4}{b} \\ $$$$=\mathrm{2}\left({a}^{\mathrm{2}} +{a}+\frac{\mathrm{1}}{\mathrm{4}}\right)+{b}^{\mathrm{2}} −\mathrm{4}{b}+\mathrm{4}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4} \\ $$$$=\mathrm{2}\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({b}−\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${max}=\mathrm{2}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(−\mathrm{4}−\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{44} \\ $$$${min}=\mathrm{2}\left(\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}=−\mathrm{3} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply