Menu Close

Question-128944

Tinku Tara 0 Comments
Pin




Question Number 128944 by ajfour last updated on 11/Jan/21
Commented by ajfour last updated on 11/Jan/21
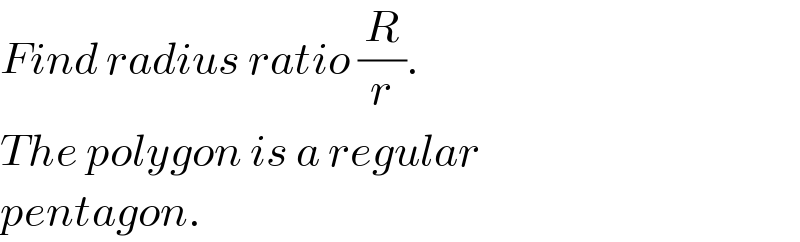
Find radius ratio (R/r). The polygon is a regular pentagon.
$${Find}\:{radius}\:{ratio}\:\frac{{R}}{{r}}. \\ $$$${The}\:{polygon}\:{is}\:{a}\:{regular} \\ $$$${pentagon}. \\ $$
Answered by mr W last updated on 11/Jan/21
Commented by mr W last updated on 11/Jan/21
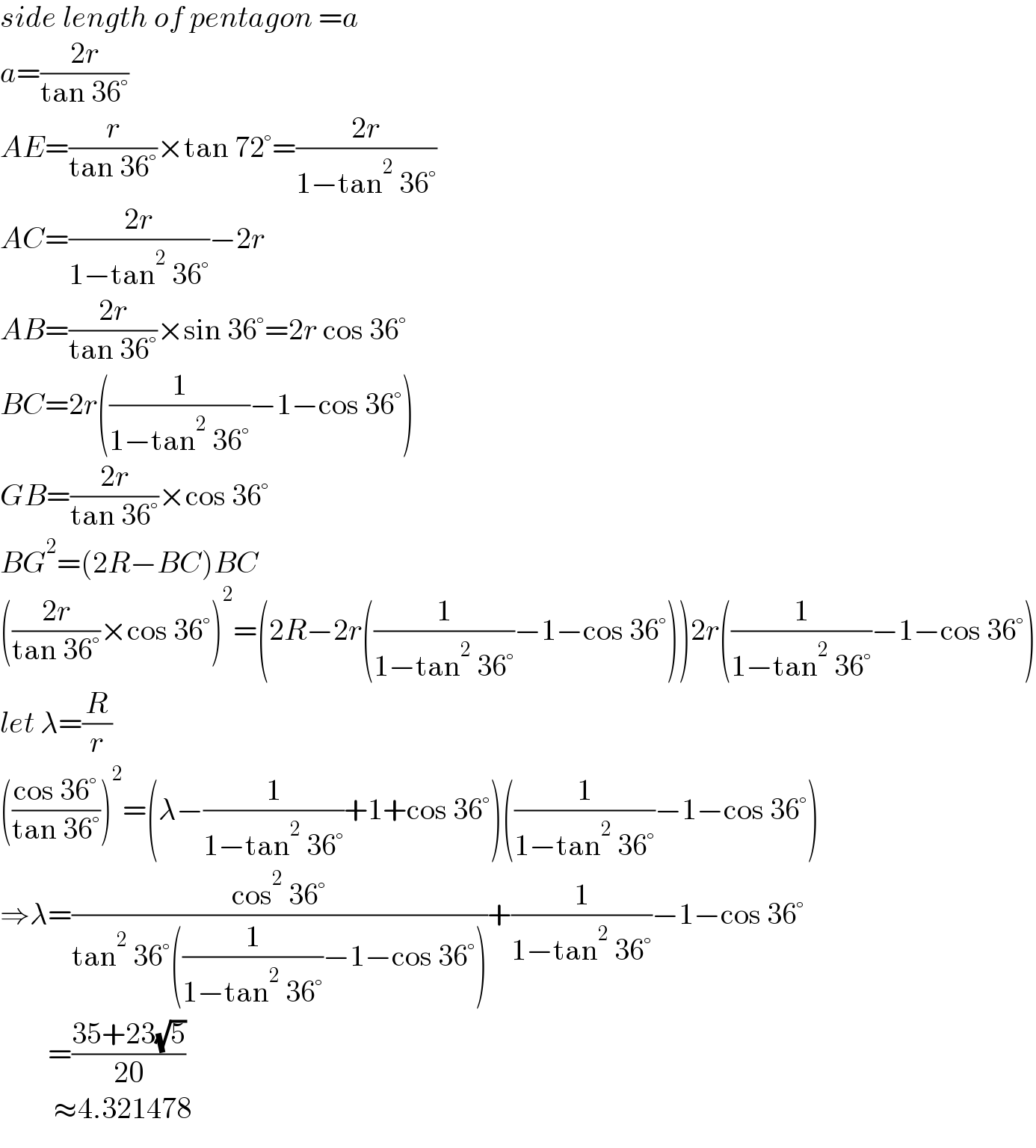
side length of pentagon =a a=((2r)/(tan 36°)) AE=(r/(tan 36°))×tan 72°=((2r)/(1−tan^2 36°)) AC=((2r)/(1−tan^2 36°))−2r AB=((2r)/(tan 36°))×sin 36°=2r cos 36° BC=2r((1/(1−tan^2 36°))−1−cos 36°) GB=((2r)/(tan 36°))×cos 36° BG^2 =(2R−BC)BC (((2r)/(tan 36°))×cos 36°)^2 =(2R−2r((1/(1−tan^2 36°))−1−cos 36°))2r((1/(1−tan^2 36°))−1−cos 36°) let λ=(R/r) (((cos 36°)/(tan 36°)))^2 =(λ−(1/(1−tan^2 36°))+1+cos 36°)((1/(1−tan^2 36°))−1−cos 36°) ⇒λ=((cos^2 36°)/(tan^2 36°((1/(1−tan^2 36°))−1−cos 36°)))+(1/(1−tan^2 36°))−1−cos 36° =((35+23(√5))/(20)) ≈4.321478
$${side}\:{length}\:{of}\:{pentagon}\:={a} \\ $$$${a}=\frac{\mathrm{2}{r}}{\mathrm{tan}\:\mathrm{36}°} \\ $$$${AE}=\frac{{r}}{\mathrm{tan}\:\mathrm{36}°}×\mathrm{tan}\:\mathrm{72}°=\frac{\mathrm{2}{r}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°} \\ $$$${AC}=\frac{\mathrm{2}{r}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{2}{r} \\ $$$${AB}=\frac{\mathrm{2}{r}}{\mathrm{tan}\:\mathrm{36}°}×\mathrm{sin}\:\mathrm{36}°=\mathrm{2}{r}\:\mathrm{cos}\:\mathrm{36}° \\ $$$${BC}=\mathrm{2}{r}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}°\right) \\ $$$${GB}=\frac{\mathrm{2}{r}}{\mathrm{tan}\:\mathrm{36}°}×\mathrm{cos}\:\mathrm{36}° \\ $$$${BG}^{\mathrm{2}} =\left(\mathrm{2}{R}−{BC}\right){BC} \\ $$$$\left(\frac{\mathrm{2}{r}}{\mathrm{tan}\:\mathrm{36}°}×\mathrm{cos}\:\mathrm{36}°\right)^{\mathrm{2}} =\left(\mathrm{2}{R}−\mathrm{2}{r}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}°\right)\right)\mathrm{2}{r}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}°\right) \\ $$$${let}\:\lambda=\frac{{R}}{{r}} \\ $$$$\left(\frac{\mathrm{cos}\:\mathrm{36}°}{\mathrm{tan}\:\mathrm{36}°}\right)^{\mathrm{2}} =\left(\lambda−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}+\mathrm{1}+\mathrm{cos}\:\mathrm{36}°\right)\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}°\right) \\ $$$$\Rightarrow\lambda=\frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{36}°}{\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}°\right)}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}−\mathrm{1}−\mathrm{cos}\:\mathrm{36}° \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{35}+\mathrm{23}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$$\:\:\:\:\:\:\:\:\:\approx\mathrm{4}.\mathrm{321478} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *