Question-129098

Question Number 129098 by Adel last updated on 12/Jan/21

Answered by liberty last updated on 12/Jan/21

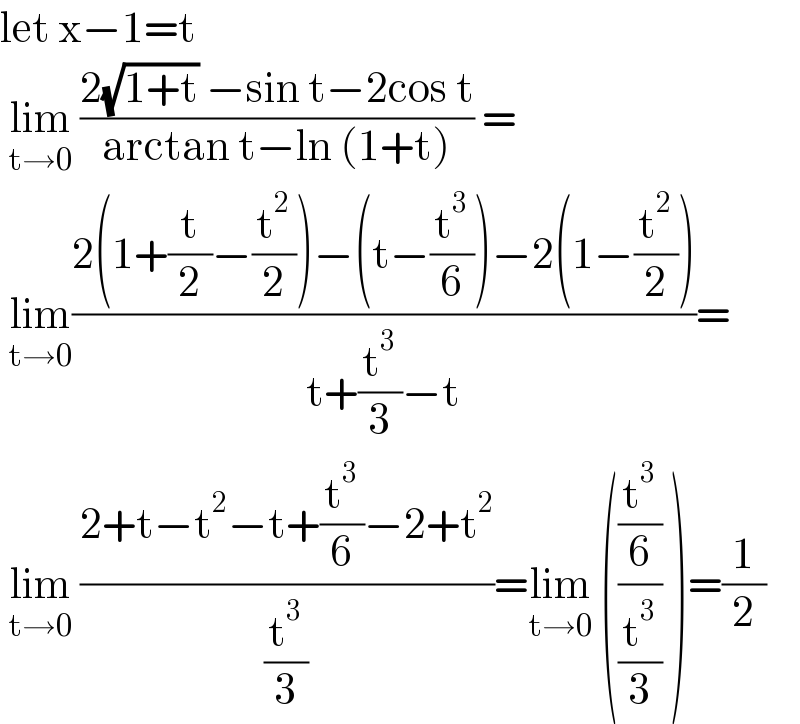
let x−1=t lim_(t→0) ((2(√(1+t)) −sin t−2cos t)/(arctan t−ln (1+t))) = lim_(t→0) ((2(1+(t/2)−(t^2 /2))−(t−(t^3 /6))−2(1−(t^2 /2)))/(t+(t^3 /3)−t))= lim_(t→0) ((2+t−t^2 −t+(t^3 /6)−2+t^2 )/(t^3 /3))=lim_(t→0) (((t^3 /6)/(t^3 /3)) )=(1/2)

$$\mathrm{let}\:\mathrm{x}−\mathrm{1}=\mathrm{t} \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{t}}\:−\mathrm{sin}\:\mathrm{t}−\mathrm{2cos}\:\mathrm{t}}{\mathrm{arctan}\:\mathrm{t}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{t}\right)}\:= \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{2}}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)−\left(\mathrm{t}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}\right)−\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{t}+\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{t}}= \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}+\mathrm{t}−\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{2}+\mathrm{t}^{\mathrm{2}} }{\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}}{\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}}\:\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Adel last updated on 13/Jan/21

$$\mathrm{tanks} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply