Question Number 129187 by math178 last updated on 13/Jan/21

Commented by math178 last updated on 13/Jan/21
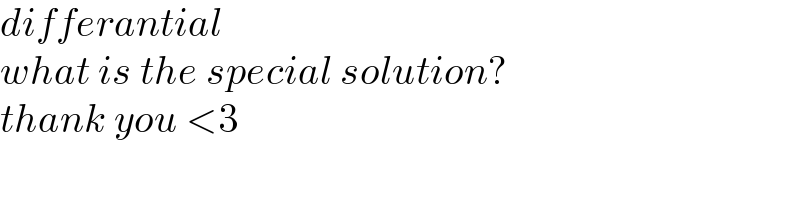
$${differantial} \\ $$$${what}\:{is}\:{the}\:{special}\:{solution}? \\ $$$${thank}\:{you}\:<\mathrm{3} \\ $$
Answered by Olaf last updated on 13/Jan/21
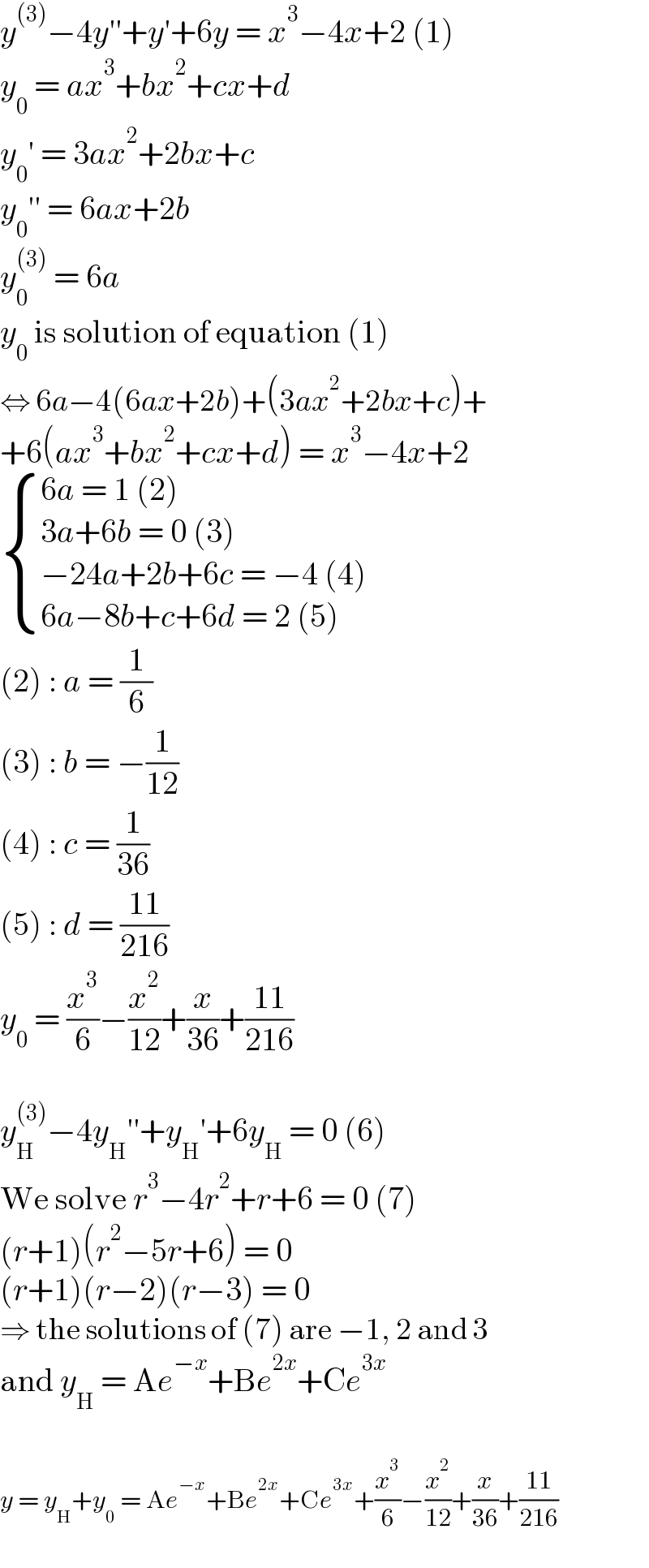
$${y}^{\left(\mathrm{3}\right)} −\mathrm{4}{y}''+{y}'+\mathrm{6}{y}\:=\:{x}^{\mathrm{3}} −\mathrm{4}{x}+\mathrm{2}\:\left(\mathrm{1}\right) \\ $$$${y}_{\mathrm{0}} \:=\:{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${y}_{\mathrm{0}} '\:=\:\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c} \\ $$$${y}_{\mathrm{0}} ''\:=\:\mathrm{6}{ax}+\mathrm{2}{b} \\ $$$${y}_{\mathrm{0}} ^{\left(\mathrm{3}\right)} \:=\:\mathrm{6}{a} \\ $$$${y}_{\mathrm{0}} \:\mathrm{is}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{equation}\:\left(\mathrm{1}\right) \\ $$$$\Leftrightarrow\:\mathrm{6}{a}−\mathrm{4}\left(\mathrm{6}{ax}+\mathrm{2}{b}\right)+\left(\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}\right)+ \\ $$$$+\mathrm{6}\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\right)\:=\:{x}^{\mathrm{3}} −\mathrm{4}{x}+\mathrm{2} \\ $$$$\begin{cases}{\mathrm{6}{a}\:=\:\mathrm{1}\:\left(\mathrm{2}\right)}\\{\mathrm{3}{a}+\mathrm{6}{b}\:=\:\mathrm{0}\:\left(\mathrm{3}\right)}\\{−\mathrm{24}{a}+\mathrm{2}{b}+\mathrm{6}{c}\:=\:−\mathrm{4}\:\left(\mathrm{4}\right)}\\{\mathrm{6}{a}−\mathrm{8}{b}+{c}+\mathrm{6}{d}\:=\:\mathrm{2}\:\left(\mathrm{5}\right)}\end{cases} \\ $$$$\left(\mathrm{2}\right)\::\:{a}\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\left(\mathrm{3}\right)\::\:{b}\:=\:−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\left(\mathrm{4}\right)\::\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\left(\mathrm{5}\right)\::\:{d}\:=\:\frac{\mathrm{11}}{\mathrm{216}} \\ $$$${y}_{\mathrm{0}} \:=\:\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{{x}^{\mathrm{2}} }{\mathrm{12}}+\frac{{x}}{\mathrm{36}}+\frac{\mathrm{11}}{\mathrm{216}} \\ $$$$ \\ $$$${y}_{\mathrm{H}} ^{\left(\mathrm{3}\right)} −\mathrm{4}{y}_{\mathrm{H}} ''+{y}_{\mathrm{H}} '+\mathrm{6}{y}_{\mathrm{H}} \:=\:\mathrm{0}\:\left(\mathrm{6}\right) \\ $$$$\mathrm{We}\:\mathrm{solve}\:{r}^{\mathrm{3}} −\mathrm{4}{r}^{\mathrm{2}} +{r}+\mathrm{6}\:=\:\mathrm{0}\:\left(\mathrm{7}\right) \\ $$$$\left({r}+\mathrm{1}\right)\left({r}^{\mathrm{2}} −\mathrm{5}{r}+\mathrm{6}\right)\:=\:\mathrm{0} \\ $$$$\left({r}+\mathrm{1}\right)\left({r}−\mathrm{2}\right)\left({r}−\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\left(\mathrm{7}\right)\:\mathrm{are}\:−\mathrm{1},\:\mathrm{2}\:\mathrm{and}\:\mathrm{3} \\ $$$$\mathrm{and}\:{y}_{\mathrm{H}} \:=\:\mathrm{A}{e}^{−{x}} +\mathrm{B}{e}^{\mathrm{2}{x}} +\mathrm{C}{e}^{\mathrm{3}{x}} \\ $$$$ \\ $$$${y}\:=\:{y}_{\mathrm{H}} +{y}_{\mathrm{0}} \:=\:\mathrm{A}{e}^{−{x}} +\mathrm{B}{e}^{\mathrm{2}{x}} +\mathrm{C}{e}^{\mathrm{3}{x}} +\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{{x}^{\mathrm{2}} }{\mathrm{12}}+\frac{{x}}{\mathrm{36}}+\frac{\mathrm{11}}{\mathrm{216}} \\ $$
Commented by math178 last updated on 13/Jan/21

$$\left.{thank}\:{you}\:=\right) \\ $$
