Menu Close

Question-129251

Tinku Tara 0 Comments
Pin




Question Number 129251 by bemath last updated on 14/Jan/21
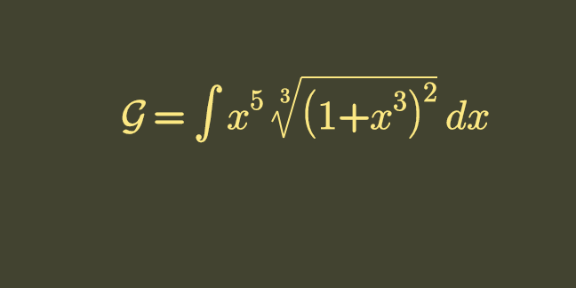
Commented by bemath last updated on 14/Jan/21
thank you all sirs
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all}\:\mathrm{sirs} \\ $$
Answered by liberty last updated on 14/Jan/21
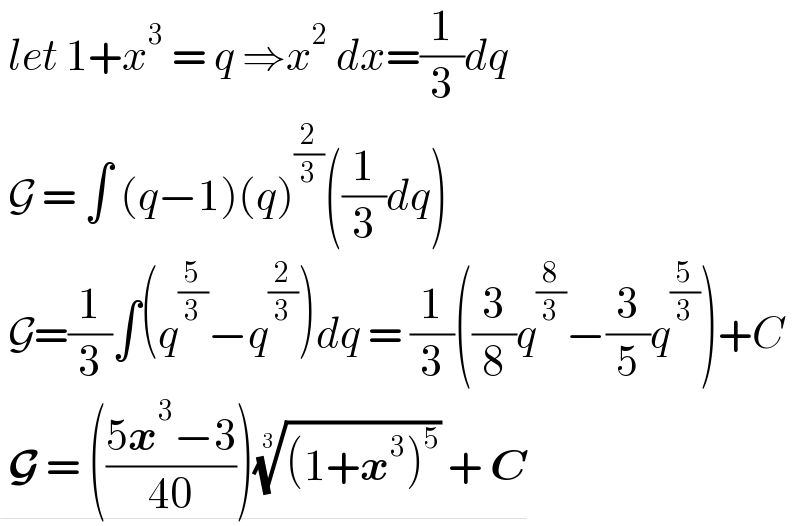
let 1+x^3 = q ⇒x^2 dx=(1/3)dq G = ∫ (q−1)(q)^(2/3) ((1/3)dq) G=(1/3)∫(q^(5/3) −q^(2/3) )dq = (1/3)((3/8)q^(8/3) −(3/5)q^(5/3) )+C G = (((5x^3 −3)/(40)))(((1+x^3 )^5 ))^(1/3) + C
$$\:{let}\:\mathrm{1}+{x}^{\mathrm{3}} \:=\:{q}\:\Rightarrow{x}^{\mathrm{2}} \:{dx}=\frac{\mathrm{1}}{\mathrm{3}}{dq}\: \\ $$$$\:\mathcal{G}\:=\:\int\:\left({q}−\mathrm{1}\right)\left({q}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\frac{\mathrm{1}}{\mathrm{3}}{dq}\right) \\ $$$$\:\mathcal{G}=\frac{\mathrm{1}}{\mathrm{3}}\int\left({q}^{\frac{\mathrm{5}}{\mathrm{3}}} −{q}^{\frac{\mathrm{2}}{\mathrm{3}}} \right){dq}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{3}}{\mathrm{8}}{q}^{\frac{\mathrm{8}}{\mathrm{3}}} −\frac{\mathrm{3}}{\mathrm{5}}{q}^{\frac{\mathrm{5}}{\mathrm{3}}} \right)+{C} \\ $$$$\underline{\:\boldsymbol{\mathcal{G}}\:=\:\left(\frac{\mathrm{5}\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{3}}{\mathrm{40}}\right)\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{3}} \right)^{\mathrm{5}} }\:+\:\boldsymbol{{C}}} \\ $$
Answered by Lordose last updated on 14/Jan/21
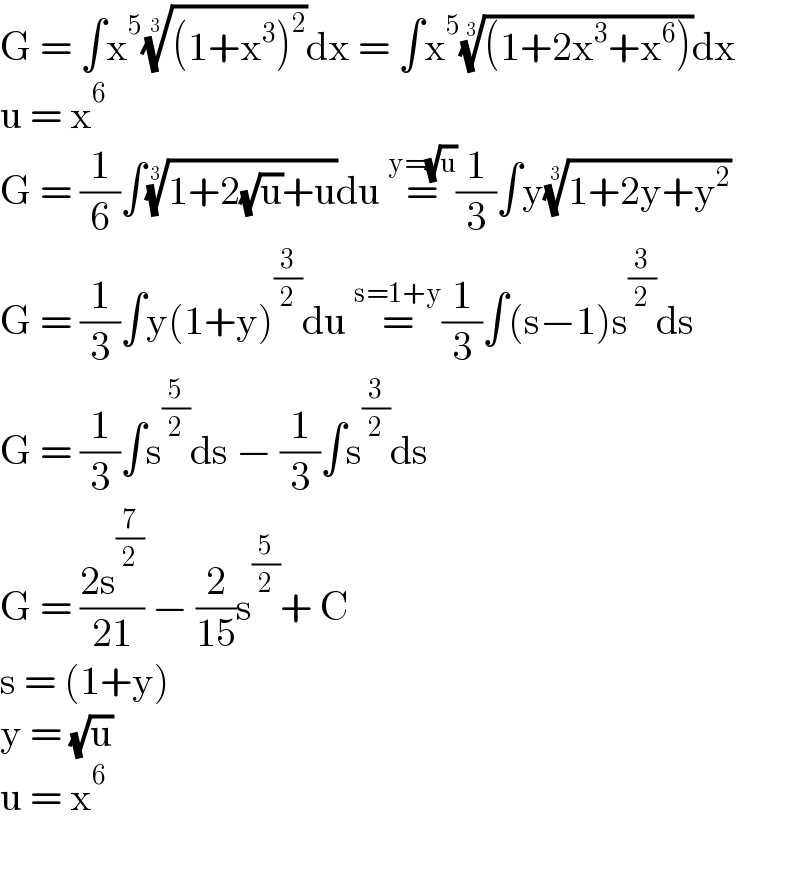
G = ∫x^5 (((1+x^3 )^2 ))^(1/3) dx = ∫x^5 (((1+2x^3 +x^6 )))^(1/3) dx u = x^6 G = (1/6)∫((1+2(√u)+u))^(1/3) du =^(y=(√u)) (1/3)∫y((1+2y+y^2 ))^(1/3) G = (1/3)∫y(1+y)^(3/2) du =^(s=1+y) (1/3)∫(s−1)s^(3/2) ds G = (1/3)∫s^(5/2) ds − (1/3)∫s^(3/2) ds G = ((2s^(7/2) )/(21)) − (2/(15))s^(5/2) + C s = (1+y) y = (√u) u = x^6
$$\mathrm{G}\:=\:\int\mathrm{x}^{\mathrm{5}} \sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\:\int\mathrm{x}^{\mathrm{5}} \sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{6}} \right)}\mathrm{dx} \\ $$$$\mathrm{u}\:=\:\mathrm{x}^{\mathrm{6}} \\ $$$$\mathrm{G}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\int\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{u}}+\mathrm{u}}\mathrm{du}\:\overset{\mathrm{y}=\sqrt{\mathrm{u}}} {=}\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{y}\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{2y}+\mathrm{y}^{\mathrm{2}} }\: \\ $$$$\mathrm{G}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{y}\left(\mathrm{1}+\mathrm{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{du}\:\overset{\mathrm{s}=\mathrm{1}+\mathrm{y}} {=}\frac{\mathrm{1}}{\mathrm{3}}\int\left(\mathrm{s}−\mathrm{1}\right)\mathrm{s}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{ds}\: \\ $$$$\mathrm{G}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{s}^{\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{ds}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{s}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{ds} \\ $$$$\mathrm{G}\:=\:\frac{\mathrm{2s}^{\frac{\mathrm{7}}{\mathrm{2}}} }{\mathrm{21}}\:−\:\frac{\mathrm{2}}{\mathrm{15}}\mathrm{s}^{\frac{\mathrm{5}}{\mathrm{2}}} +\:\mathrm{C} \\ $$$$\mathrm{s}\:=\:\left(\mathrm{1}+\mathrm{y}\right) \\ $$$$\mathrm{y}\:=\:\sqrt{\mathrm{u}} \\ $$$$\mathrm{u}\:=\:\mathrm{x}^{\mathrm{6}} \\ $$$$ \\ $$
Answered by Olaf last updated on 14/Jan/21
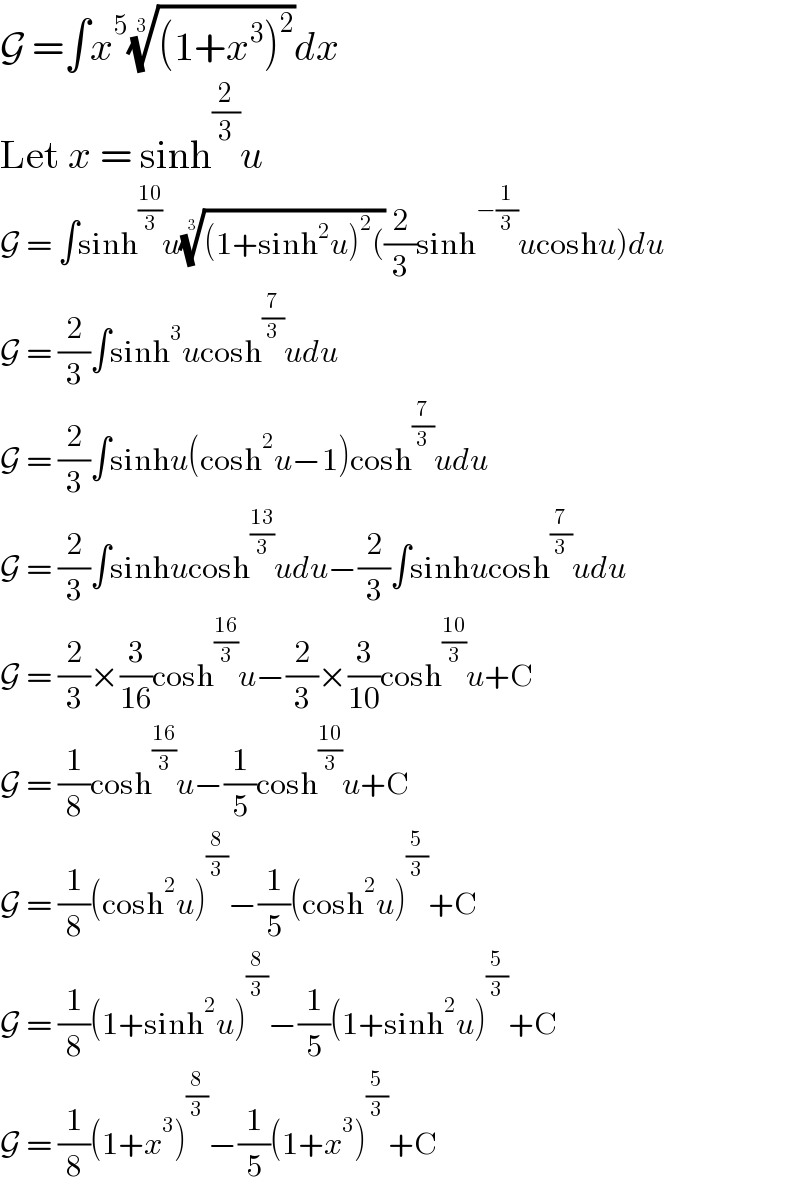
G =∫x^5 (((1+x^3 )^2 ))^(1/3) dx Let x = sinh^(2/3) u G = ∫sinh^((10)/3) u(((1+sinh^2 u)^2 ())^(1/3) (2/3)sinh^(−(1/3)) ucoshu)du G = (2/3)∫sinh^3 ucosh^(7/3) udu G = (2/3)∫sinhu(cosh^2 u−1)cosh^(7/3) udu G = (2/3)∫sinhucosh^((13)/3) udu−(2/3)∫sinhucosh^(7/3) udu G = (2/3)×(3/(16))cosh^((16)/3) u−(2/3)×(3/(10))cosh^((10)/3) u+C G = (1/8)cosh^((16)/3) u−(1/5)cosh^((10)/3) u+C G = (1/8)(cosh^2 u)^(8/3) −(1/5)(cosh^2 u)^(5/3) +C G = (1/8)(1+sinh^2 u)^(8/3) −(1/5)(1+sinh^2 u)^(5/3) +C G = (1/8)(1+x^3 )^(8/3) −(1/5)(1+x^3 )^(5/3) +C
$$\mathcal{G}\:=\int{x}^{\mathrm{5}} \sqrt[{\mathrm{3}}]{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{sinh}^{\frac{\mathrm{2}}{\mathrm{3}}} {u} \\ $$$$\left.\mathcal{G}\:=\:\int\mathrm{sinh}^{\frac{\mathrm{10}}{\mathrm{3}}} {u}\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} {u}\right)^{\mathrm{2}} \left(\right.}\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sinh}^{−\frac{\mathrm{1}}{\mathrm{3}}} {u}\mathrm{cosh}{u}\right){du} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\mathrm{sinh}^{\mathrm{3}} {u}\mathrm{cosh}^{\frac{\mathrm{7}}{\mathrm{3}}} {udu} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\mathrm{sinh}{u}\left(\mathrm{cosh}^{\mathrm{2}} {u}−\mathrm{1}\right)\mathrm{cosh}^{\frac{\mathrm{7}}{\mathrm{3}}} {udu} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\mathrm{sinh}{u}\mathrm{cosh}^{\frac{\mathrm{13}}{\mathrm{3}}} {udu}−\frac{\mathrm{2}}{\mathrm{3}}\int\mathrm{sinh}{u}\mathrm{cosh}^{\frac{\mathrm{7}}{\mathrm{3}}} {udu} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{16}}\mathrm{cosh}^{\frac{\mathrm{16}}{\mathrm{3}}} {u}−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{10}}\mathrm{cosh}^{\frac{\mathrm{10}}{\mathrm{3}}} {u}+\mathrm{C} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cosh}^{\frac{\mathrm{16}}{\mathrm{3}}} {u}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cosh}^{\frac{\mathrm{10}}{\mathrm{3}}} {u}+\mathrm{C} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{cosh}^{\mathrm{2}} {u}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{cosh}^{\mathrm{2}} {u}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} +\mathrm{C} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} {u}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} {u}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} +\mathrm{C} \\ $$$$\mathcal{G}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{8}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{5}}{\mathrm{3}}} +\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *