Menu Close

Question-129364

Tinku Tara 0 Comments
Pin




Question Number 129364 by shaker last updated on 15/Jan/21
Answered by mindispower last updated on 15/Jan/21
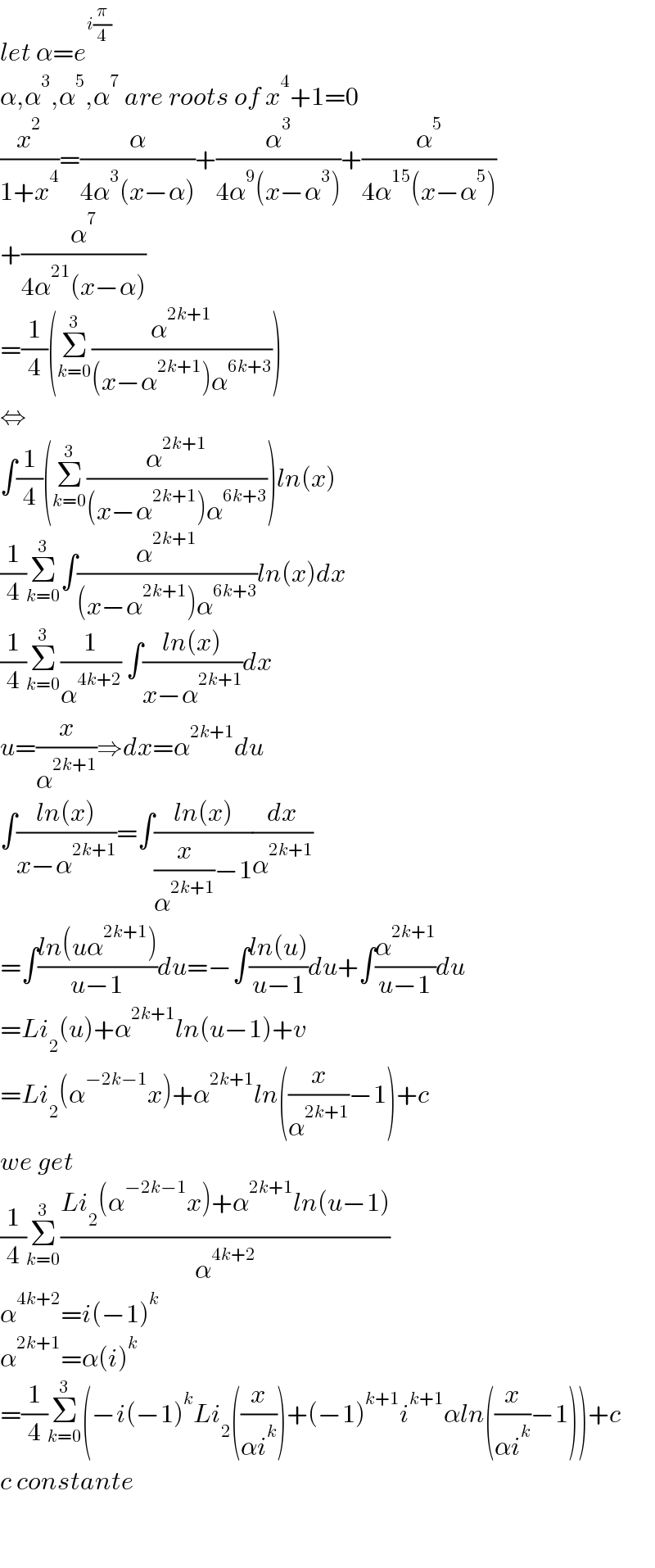
let α=e^(i(π/4)) α,α^3 ,α^5 ,α^7 are roots of x^4 +1=0 (x^2 /(1+x^4 ))=(α/(4α^3 (x−α)))+(α^3 /(4α^9 (x−α^3 )))+(α^5 /(4α^(15) (x−α^5 ))) +(α^7 /(4α^(21) (x−α))) =(1/4)(Σ_(k=0) ^3 (α^(2k+1) /((x−α^(2k+1) )α^(6k+3) ))) ⇔ ∫(1/4)(Σ_(k=0) ^3 (α^(2k+1) /((x−α^(2k+1) )α^(6k+3) )))ln(x) (1/4)Σ_(k=0) ^3 ∫(α^(2k+1) /((x−α^(2k+1) )α^(6k+3) ))ln(x)dx (1/4)Σ_(k=0) ^3 (1/α^(4k+2) ) ∫((ln(x))/(x−α^(2k+1) ))dx u=(x/α^(2k+1) )⇒dx=α^(2k+1) du ∫((ln(x))/(x−α^(2k+1) ))=∫((ln(x))/((x/α^(2k+1) )−1))(dx/α^(2k+1) ) =∫((ln(uα^(2k+1) ))/(u−1))du=−∫((ln(u))/(u−1))du+∫(α^(2k+1) /(u−1))du =Li_2 (u)+α^(2k+1) ln(u−1)+v =Li_2 (α^(−2k−1) x)+α^(2k+1) ln((x/α^(2k+1) )−1)+c we get (1/4)Σ_(k=0) ^3 ((Li_2 (α^(−2k−1) x)+α^(2k+1) ln(u−1))/α^(4k+2) ) α^(4k+2) =i(−1)^k α^(2k+1) =α(i)^k =(1/4)Σ_(k=0) ^3 (−i(−1)^k Li_2 ((x/(αi^k )))+(−1)^(k+1) i^(k+1) αln((x/(αi^k ))−1))+c c constante
$${let}\:\alpha={e}^{{i}\frac{\pi}{\mathrm{4}}} \\ $$$$\alpha,\alpha^{\mathrm{3}} ,\alpha^{\mathrm{5}} ,\alpha^{\mathrm{7}} \:{are}\:{roots}\:{of}\:{x}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }=\frac{\alpha}{\mathrm{4}\alpha^{\mathrm{3}} \left({x}−\alpha\right)}+\frac{\alpha^{\mathrm{3}} }{\mathrm{4}\alpha^{\mathrm{9}} \left({x}−\alpha^{\mathrm{3}} \right)}+\frac{\alpha^{\mathrm{5}} }{\mathrm{4}\alpha^{\mathrm{15}} \left({x}−\alpha^{\mathrm{5}} \right)} \\ $$$$+\frac{\alpha^{\mathrm{7}} }{\mathrm{4}\alpha^{\mathrm{21}} \left({x}−\alpha\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\frac{\alpha^{\mathrm{2}{k}+\mathrm{1}} }{\left({x}−\alpha^{\mathrm{2}{k}+\mathrm{1}} \right)\alpha^{\mathrm{6}{k}+\mathrm{3}} }\right) \\ $$$$\Leftrightarrow \\ $$$$\int\frac{\mathrm{1}}{\mathrm{4}}\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\frac{\alpha^{\mathrm{2}{k}+\mathrm{1}} }{\left({x}−\alpha^{\mathrm{2}{k}+\mathrm{1}} \right)\alpha^{\mathrm{6}{k}+\mathrm{3}} }\right){ln}\left({x}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\int\frac{\alpha^{\mathrm{2}{k}+\mathrm{1}} }{\left({x}−\alpha^{\mathrm{2}{k}+\mathrm{1}} \right)\alpha^{\mathrm{6}{k}+\mathrm{3}} }{ln}\left({x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\frac{\mathrm{1}}{\alpha^{\mathrm{4}{k}+\mathrm{2}} }\:\int\frac{{ln}\left({x}\right)}{{x}−\alpha^{\mathrm{2}{k}+\mathrm{1}} }{dx} \\ $$$${u}=\frac{{x}}{\alpha^{\mathrm{2}{k}+\mathrm{1}} }\Rightarrow{dx}=\alpha^{\mathrm{2}{k}+\mathrm{1}} {du} \\ $$$$\int\frac{{ln}\left({x}\right)}{{x}−\alpha^{\mathrm{2}{k}+\mathrm{1}} }=\int\frac{{ln}\left({x}\right)}{\frac{{x}}{\alpha^{\mathrm{2}{k}+\mathrm{1}} }−\mathrm{1}}\frac{{dx}}{\alpha^{\mathrm{2}{k}+\mathrm{1}} } \\ $$$$=\int\frac{{ln}\left({u}\alpha^{\mathrm{2}{k}+\mathrm{1}} \right)}{{u}−\mathrm{1}}{du}=−\int\frac{{ln}\left({u}\right)}{{u}−\mathrm{1}}{du}+\int\frac{\alpha^{\mathrm{2}{k}+\mathrm{1}} }{{u}−\mathrm{1}}{du} \\ $$$$={Li}_{\mathrm{2}} \left({u}\right)+\alpha^{\mathrm{2}{k}+\mathrm{1}} {ln}\left({u}−\mathrm{1}\right)+{v} \\ $$$$={Li}_{\mathrm{2}} \left(\alpha^{−\mathrm{2}{k}−\mathrm{1}} {x}\right)+\alpha^{\mathrm{2}{k}+\mathrm{1}} {ln}\left(\frac{{x}}{\alpha^{\mathrm{2}{k}+\mathrm{1}} }−\mathrm{1}\right)+{c} \\ $$$${we}\:{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\frac{{Li}_{\mathrm{2}} \left(\alpha^{−\mathrm{2}{k}−\mathrm{1}} {x}\right)+\alpha^{\mathrm{2}{k}+\mathrm{1}} {ln}\left({u}−\mathrm{1}\right)}{\alpha^{\mathrm{4}{k}+\mathrm{2}} } \\ $$$$\alpha^{\mathrm{4}{k}+\mathrm{2}} ={i}\left(−\mathrm{1}\right)^{{k}} \\ $$$$\alpha^{\mathrm{2}{k}+\mathrm{1}} =\alpha\left({i}\right)^{{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\left(−{i}\left(−\mathrm{1}\right)^{{k}} {Li}_{\mathrm{2}} \left(\frac{{x}}{\alpha{i}^{{k}} }\right)+\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {i}^{{k}+\mathrm{1}} \alpha{ln}\left(\frac{{x}}{\alpha{i}^{{k}} }−\mathrm{1}\right)\right)+{c} \\ $$$${c}\:{constante} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *