Question Number 129367 by BHOOPENDRA last updated on 15/Jan/21
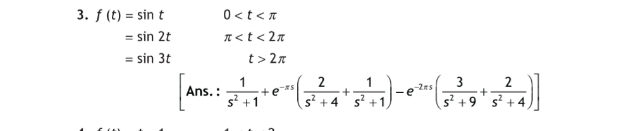
Commented by BHOOPENDRA last updated on 15/Jan/21
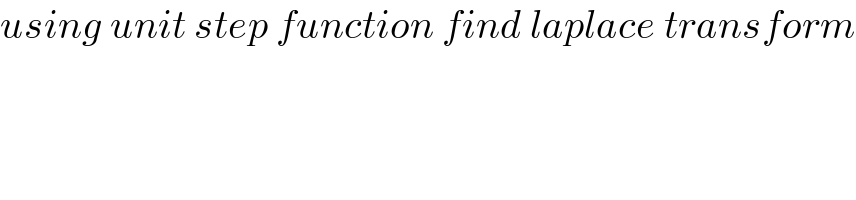
$${using}\:{unit}\:{step}\:{function}\:{find}\:{laplace}\:{transform} \\ $$
Answered by mathmax by abdo last updated on 15/Jan/21
![L(f(t))=∫_0 ^∞ f(x)e^(−xt) dx =∫_0 ^π f(x)e^(−xt) dx+∫_π ^(2π) f(x)e^(−xt) dx+∫_(2π) ^(+∞) f(x)e^(−xt) dx =∫_0 ^π sinx e^(−xt) dx +∫_π ^(2π) sin(2x)e^(−xt) dx+∫_(2π) ^∞ sin(3x)e^(−xt) dx we hsve ∫_0 ^π e^(−xt) sinx dx =Im(∫_0 ^π e^(−xt+ix) dx) a7d ∫_0 ^π e^((−t+i)x) dx =[(1/(−t+i))e^((−t+i)x) ]_0 ^π =−(1/(t−i)){e^((−t+i)π) −1} =−((t+i)/(t^2 +1)){−e^(−πt) −1} =((t+i)/(t^2 +1))(1+e^(−πt) ) ⇒ ∫_0 ^π e^(−tx) sinx dx =((1+e^(−πt) )/(1+t^2 )) ∫_π ^(2π) sin(2x)e^(−tx) dx =Im(∫_π ^(2π) e^(−tx+2ix) dx) and ∫_π ^(2π) e^((−t+2i)x) dx =[(1/(−t+2i))e^((−t+2i)x) ]_π ^(2π) =−(1/(t−2i)){e^((−t+2i)2π) −e^((−t+2i)π) } =−((t+2i)/(t^2 +4)){e^(−2πt) −e^(−πt) } =((t+2i)/(t^2 +4))(e^(−πt) −e^(−2πt) )⇒ ∫_π ^(2π) e^((−t+2)x) dx =(2/(t^2 +4))(e^(−πt) −e^(−2πt) ) ∫_(2π) ^∞ sin(3x)e^(−tx) dx =Im(∫_(2π) ^∞ e^(−tx+3ix) dx) ∫_(2π) ^∞ e^((−t+3i)x) dx =[(1/(−t+3i))e^((−t+3i)x) ]_(2π) ^∞ =−(1/(t−3i)){−e^((−t+3i)2π) } =((t+3i)/(t^2 +9))(e^(−2πt) ) ⇒ ∫_(2π) ^∞ sin(3x)e^(−tx) dx =((3e^(−2πt) )/(t^2 +9)) ⇒ L(f(t)) =((1+e^(−πt) )/(1+t^2 )) +(2/(t^2 +4))(e^(−πt) −e^(−2πt) )+((3e^(−2πt) )/(t^2 +9))](https://www.tinkutara.com/question/Q129382.png)
$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}+\int_{\pi} ^{\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}+\int_{\mathrm{2}\pi} ^{+\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \mathrm{sinx}\:\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}+\int_{\mathrm{2}\pi} ^{\infty} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dx}\:\mathrm{we}\:\mathrm{hsve} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{xt}} \mathrm{sinx}\:\mathrm{dx}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{xt}+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{a7d} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{t}+\mathrm{i}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\pi} \:=−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{i}}\left\{\mathrm{e}^{\left(−\mathrm{t}+\mathrm{i}\right)\pi} −\mathrm{1}\right\} \\ $$$$=−\frac{\mathrm{t}+\mathrm{i}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\left\{−\mathrm{e}^{−\pi\mathrm{t}} −\mathrm{1}\right\}\:=\frac{\mathrm{t}+\mathrm{i}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\left(\mathrm{1}+\mathrm{e}^{−\pi\mathrm{t}} \right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{tx}} \mathrm{sinx}\:\mathrm{dx}\:=\frac{\mathrm{1}+\mathrm{e}^{−\pi\mathrm{t}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=\mathrm{Im}\left(\int_{\pi} ^{\mathrm{2}\pi} \mathrm{e}^{−\mathrm{tx}+\mathrm{2ix}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{2i}}\mathrm{e}^{\left(−\mathrm{t}+\mathrm{2i}\right)\mathrm{x}} \right]_{\pi} ^{\mathrm{2}\pi} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{2i}}\left\{\mathrm{e}^{\left(−\mathrm{t}+\mathrm{2i}\right)\mathrm{2}\pi} −\mathrm{e}^{\left(−\mathrm{t}+\mathrm{2i}\right)\pi} \right\} \\ $$$$=−\frac{\mathrm{t}+\mathrm{2i}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}}\left\{\mathrm{e}^{−\mathrm{2}\pi\mathrm{t}} −\mathrm{e}^{−\pi\mathrm{t}} \right\}\:=\frac{\mathrm{t}+\mathrm{2i}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}}\left(\mathrm{e}^{−\pi\mathrm{t}} −\mathrm{e}^{−\mathrm{2}\pi\mathrm{t}} \right)\Rightarrow \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{2}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}}\left(\mathrm{e}^{−\pi\mathrm{t}} −\mathrm{e}^{−\mathrm{2}\pi\mathrm{t}} \right) \\ $$$$\int_{\mathrm{2}\pi} ^{\infty} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=\mathrm{Im}\left(\int_{\mathrm{2}\pi} ^{\infty} \:\mathrm{e}^{−\mathrm{tx}+\mathrm{3ix}} \mathrm{dx}\right) \\ $$$$\int_{\mathrm{2}\pi} ^{\infty} \:\:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{3i}\right)\mathrm{x}} \mathrm{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{3i}}\mathrm{e}^{\left(−\mathrm{t}+\mathrm{3i}\right)\mathrm{x}} \right]_{\mathrm{2}\pi} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{3i}}\left\{−\mathrm{e}^{\left(−\mathrm{t}+\mathrm{3i}\right)\mathrm{2}\pi} \right\}\:=\frac{\mathrm{t}+\mathrm{3i}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}}\left(\mathrm{e}^{−\mathrm{2}\pi\mathrm{t}} \right)\:\Rightarrow \\ $$$$\int_{\mathrm{2}\pi} ^{\infty} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=\frac{\mathrm{3e}^{−\mathrm{2}\pi\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{1}+\mathrm{e}^{−\pi\mathrm{t}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}}\left(\mathrm{e}^{−\pi\mathrm{t}} −\mathrm{e}^{−\mathrm{2}\pi\mathrm{t}} \right)+\frac{\mathrm{3e}^{−\mathrm{2}\pi\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}} \\ $$
Commented by BHOOPENDRA last updated on 15/Jan/21

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 16/Jan/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
