Question Number 129378 by BHOOPENDRA last updated on 15/Jan/21
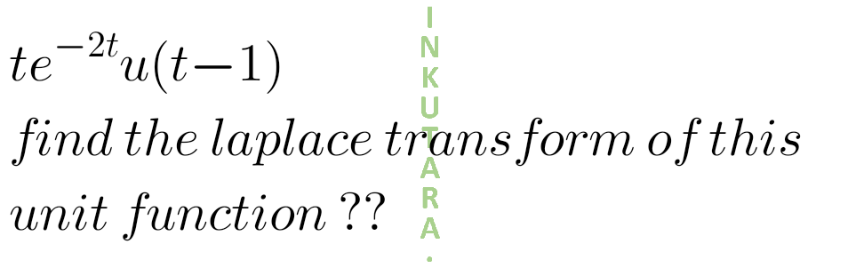
Answered by Dwaipayan Shikari last updated on 15/Jan/21
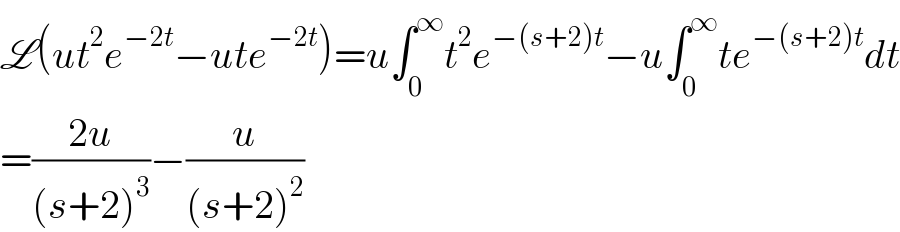
$$\mathscr{L}\left({ut}^{\mathrm{2}} {e}^{−\mathrm{2}{t}} −{ute}^{−\mathrm{2}{t}} \right)={u}\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}} {e}^{−\left({s}+\mathrm{2}\right){t}} −{u}\int_{\mathrm{0}} ^{\infty} {te}^{−\left({s}+\mathrm{2}\right){t}} {dt} \\ $$$$=\frac{\mathrm{2}{u}}{\left({s}+\mathrm{2}\right)^{\mathrm{3}} }−\frac{{u}}{\left({s}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$
