Question Number 129380 by mohammad17 last updated on 15/Jan/21

Answered by physicstutes last updated on 15/Jan/21
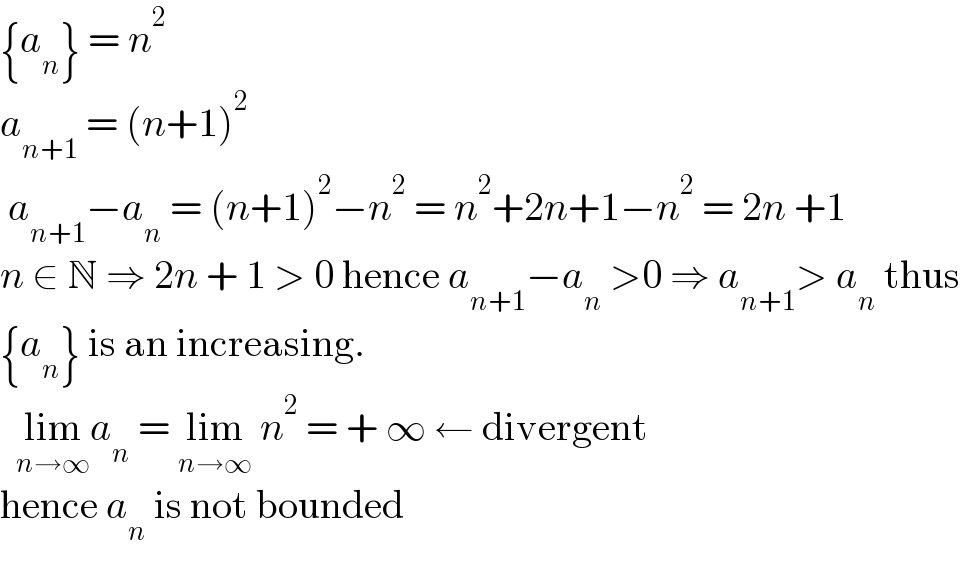
$$\left\{{a}_{{n}} \right\}\:=\:{n}^{\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} \:=\:\left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:{a}_{{n}+\mathrm{1}} −{a}_{{n}} \:=\:\left({n}+\mathrm{1}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} \:=\:{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}−{n}^{\mathrm{2}} \:=\:\mathrm{2}{n}\:+\mathrm{1} \\ $$$${n}\:\in\:\mathbb{N}\:\Rightarrow\:\mathrm{2}{n}\:+\:\mathrm{1}\:>\:\mathrm{0}\:\mathrm{hence}\:{a}_{{n}+\mathrm{1}} −{a}_{{n}} \:>\mathrm{0}\:\Rightarrow\:{a}_{{n}+\mathrm{1}} >\:{a}_{{n}} \:\mathrm{thus} \\ $$$$\left\{{a}_{{n}} \right\}\:\mathrm{is}\:\mathrm{an}\:\mathrm{increasing}. \\ $$$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} \:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{\mathrm{2}} \:=\:+\:\infty\:\leftarrow\:\mathrm{divergent} \\ $$$$\mathrm{hence}\:{a}_{{n}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{bounded} \\ $$
Commented by mohammad17 last updated on 15/Jan/21

$${very}\:{thank}\:{sir} \\ $$
