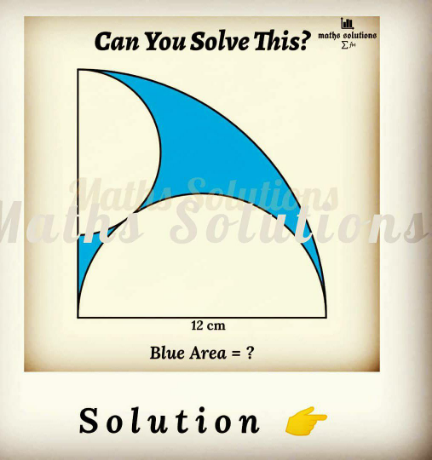
Question Number 129449 by Gulnoza last updated on 15/Jan/21
Answered by MJS_new last updated on 16/Jan/21

$$\mathrm{yes}. \\ $$
Commented by Gulnoza last updated on 16/Jan/21
ok help me , then
Commented by MJS_new last updated on 16/Jan/21
$$\left.\mathrm{sorry},\:\mathrm{I}\:\mathrm{love}\:\mathrm{to}\:\mathrm{exactly}\:\mathrm{answer}\:\mathrm{questions}\:;−\right) \\ $$
Answered by bemath last updated on 16/Jan/21

$$\mathrm{yes}…\mathrm{too} \\ $$
Answered by MJS_new last updated on 16/Jan/21
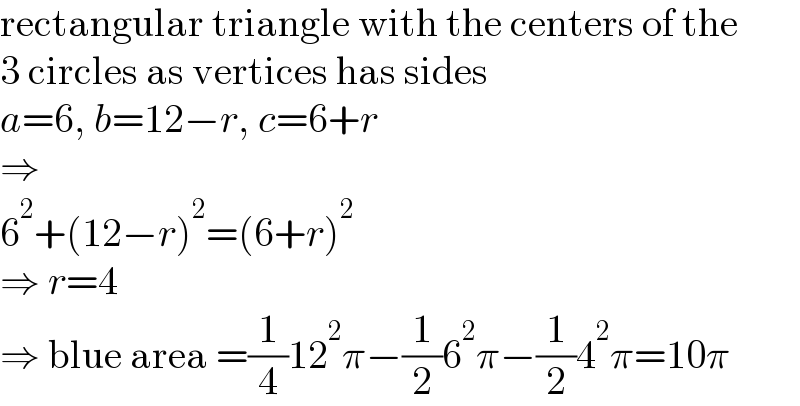
$$\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{the}\:\mathrm{centers}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{3}\:\mathrm{circles}\:\mathrm{as}\:\mathrm{vertices}\:\mathrm{has}\:\mathrm{sides} \\ $$$${a}=\mathrm{6},\:{b}=\mathrm{12}−{r},\:{c}=\mathrm{6}+{r} \\ $$$$\Rightarrow \\ $$$$\mathrm{6}^{\mathrm{2}} +\left(\mathrm{12}−{r}\right)^{\mathrm{2}} =\left(\mathrm{6}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{r}=\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{blue}\:\mathrm{area}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{12}^{\mathrm{2}} \pi−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{6}^{\mathrm{2}} \pi−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{4}^{\mathrm{2}} \pi=\mathrm{10}\pi \\ $$
