Menu Close

Question-129542

Tinku Tara 0 Comments
Pin




Question Number 129542 by mr W last updated on 16/Jan/21
Commented by mr W last updated on 16/Jan/21
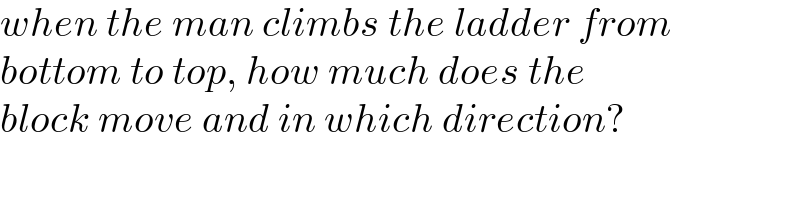
when the man climbs the ladder from bottom to top, how much does the block move and in which direction?
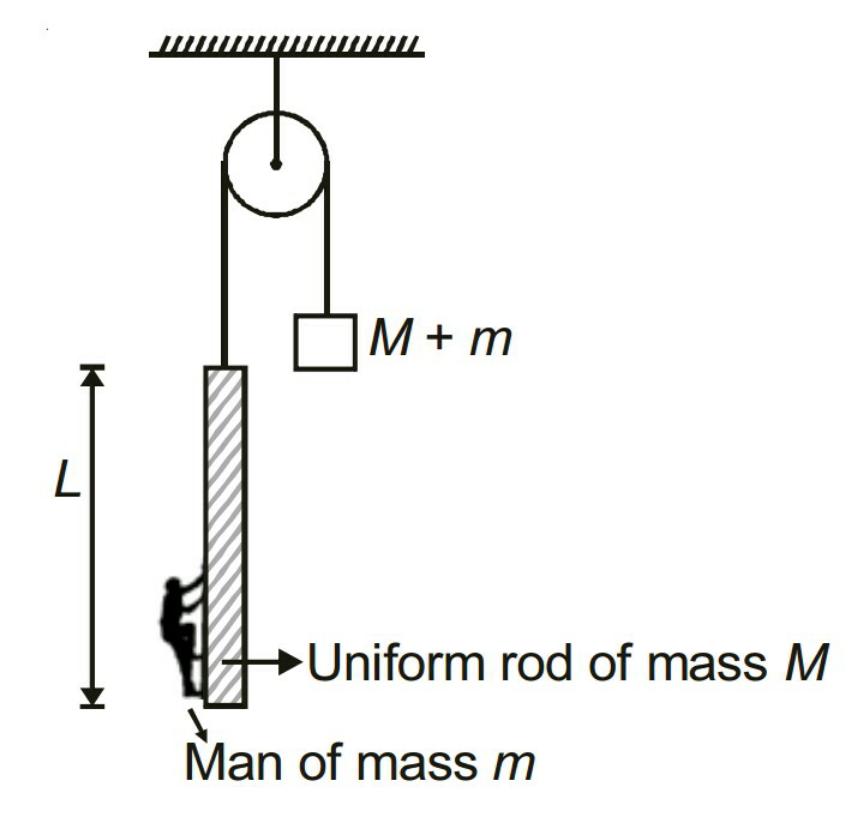
$${when}\:{the}\:{man}\:{climbs}\:{the}\:{ladder}\:{from} \\ $$$${bottom}\:{to}\:{top},\:{how}\:{much}\:{does}\:{the} \\ $$$${block}\:{move}\:{and}\:{in}\:{which}\:{direction}? \\ $$
Answered by ajfour last updated on 17/Jan/21
If man climbs ladder in time t. F−mg=ma ↑(system: man only) (system: ladder and block) F−mg=(2M+m)A ↓ (2M+m)A=ma (1/2)(A+a)t^2 =L (1/2)(1+1+((2M)/m))At^2 =L (1/2)At^2 =y dividing (y/L)=(m/(2(M+m))) y_(block) =((mL)/(2(M+m))) ↑
$${If}\:{man}\:{climbs}\:{ladder}\:{in}\:{time}\:{t}. \\ $$$${F}−{mg}={ma}\:\uparrow\left({system}:\:{man}\:{only}\right) \\ $$$$\left({system}:\:{ladder}\:{and}\:{block}\right) \\ $$$${F}−{mg}=\left(\mathrm{2}{M}+{m}\right){A}\:\downarrow\: \\ $$$$\left(\mathrm{2}{M}+{m}\right){A}={ma} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{a}\right){t}^{\mathrm{2}} ={L} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{1}+\frac{\mathrm{2}{M}}{{m}}\right){At}^{\mathrm{2}} ={L} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{At}^{\mathrm{2}} ={y} \\ $$$${dividing} \\ $$$$\frac{{y}}{{L}}=\frac{{m}}{\mathrm{2}\left({M}+{m}\right)} \\ $$$$\:\:\:{y}_{{block}} =\frac{{mL}}{\mathrm{2}\left({M}+{m}\right)}\:\:\uparrow \\ $$
Commented by mr W last updated on 16/Jan/21
great! thanks!
$${great}!\:{thanks}! \\ $$
Commented by Emptyset last updated on 17/Jan/21
can you please elaborate
$${can}\:{you}\:{please}\:{elaborate} \\ $$
Answered by mr W last updated on 17/Jan/21
Commented by mr W last updated on 17/Jan/21
T=tension in massless rope F=force between man and ladder a=acceleration of man upwards A=acceleration of block upwards =acceleration of ladder downwards system man: F−mg=ma ...(i) system ladder: F+Mg−T=MA ...(ii) system block: T−(M+m)g=(M+m)A ...(iii) (ii)+(iii): F−mg=(2M+m)A ⇒F=2(M+m)A+mg put this into (i): (2M+m)A=ma ⇒a=((2M+m)/m)×A relative acceleration between man and ladder a_R =a+A=((2(M+m))/m)×A ⇒(A/a_R )=(m/(2(M+m))) say the distance the block moves is H, H=(1/2)At^2 the distance the man moves relatively to ladder is L, L=(1/2)a_R t^2 ⇒(H/L)=(A/a_R )=(m/(2(M+m))) ⇒H=((mL)/(2(M+m))) its direction is upwards.
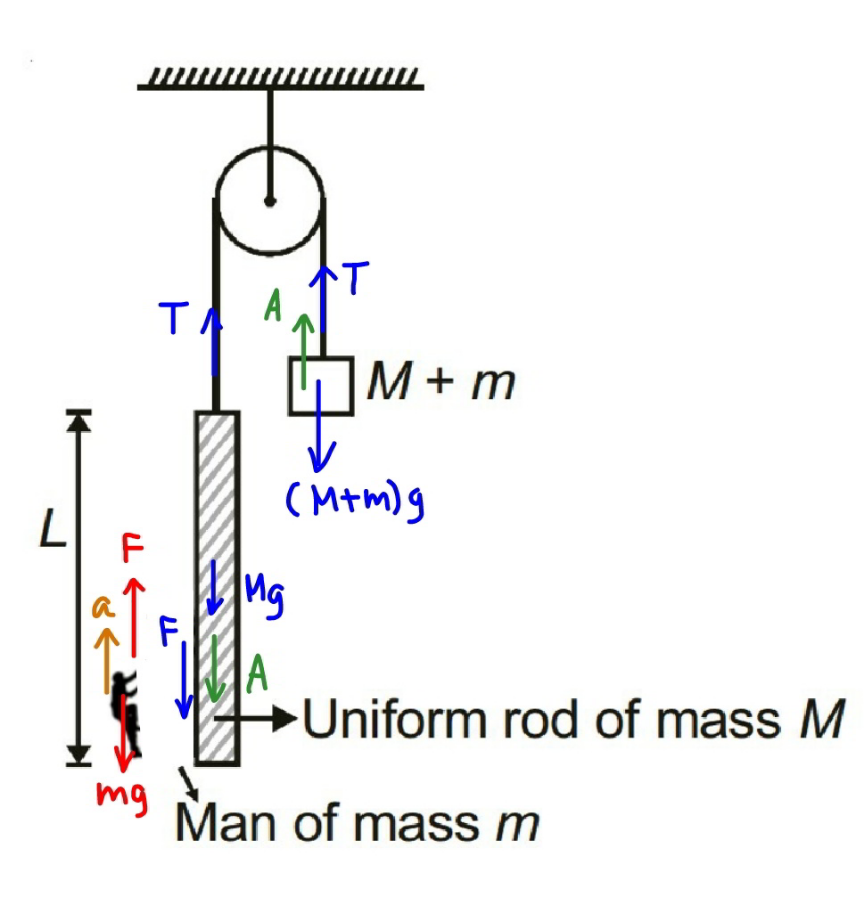
$${T}={tension}\:{in}\:{massless}\:{rope} \\ $$$${F}={force}\:{between}\:{man}\:{and}\:{ladder} \\ $$$${a}={acceleration}\:{of}\:{man}\:{upwards} \\ $$$${A}={acceleration}\:{of}\:{block}\:{upwards} \\ $$$$\:\:\:\:={acceleration}\:{of}\:{ladder}\:{downwards} \\ $$$$ \\ $$$${system}\:{man}: \\ $$$${F}−{mg}={ma}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${system}\:{ladder}: \\ $$$${F}+{Mg}−{T}={MA}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${system}\:{block}: \\ $$$${T}−\left({M}+{m}\right){g}=\left({M}+{m}\right){A}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({ii}\right)+\left({iii}\right): \\ $$$${F}−{mg}=\left(\mathrm{2}{M}+{m}\right){A} \\ $$$$\Rightarrow{F}=\mathrm{2}\left({M}+{m}\right){A}+{mg} \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\left(\mathrm{2}{M}+{m}\right){A}={ma} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2}{M}+{m}}{{m}}×{A} \\ $$$${relative}\:{acceleration}\:{between}\:{man}\: \\ $$$${and}\:{ladder}\:{a}_{{R}} ={a}+{A}=\frac{\mathrm{2}\left({M}+{m}\right)}{{m}}×{A} \\ $$$$\Rightarrow\frac{{A}}{{a}_{{R}} }=\frac{{m}}{\mathrm{2}\left({M}+{m}\right)} \\ $$$${say}\:{the}\:{distance}\:{the}\:{block}\:{moves}\:{is}\:{H}, \\ $$$${H}=\frac{\mathrm{1}}{\mathrm{2}}{At}^{\mathrm{2}} \\ $$$${the}\:{distance}\:{the}\:{man}\:{moves}\:{relatively} \\ $$$${to}\:{ladder}\:{is}\:{L}, \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{2}}{a}_{{R}} {t}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{H}}{{L}}=\frac{{A}}{{a}_{{R}} }=\frac{{m}}{\mathrm{2}\left({M}+{m}\right)} \\ $$$$\Rightarrow{H}=\frac{{mL}}{\mathrm{2}\left({M}+{m}\right)} \\ $$$${its}\:{direction}\:{is}\:{upwards}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *