Question Number 129568 by abdurehime last updated on 16/Jan/21
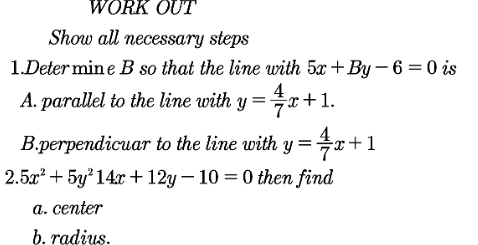
Commented by greg_ed last updated on 16/Jan/21

$$\boldsymbol{\mathrm{please}},\:\boldsymbol{\mathrm{review}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{question}}\:\mathrm{2}\:! \\ $$$$\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{seems}}\:+\:\boldsymbol{\mathrm{or}}\:−\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{missed}}\:\boldsymbol{\mathrm{before}}\:\mathrm{14}\boldsymbol{{x}}. \\ $$
Commented by bemath last updated on 17/Jan/21
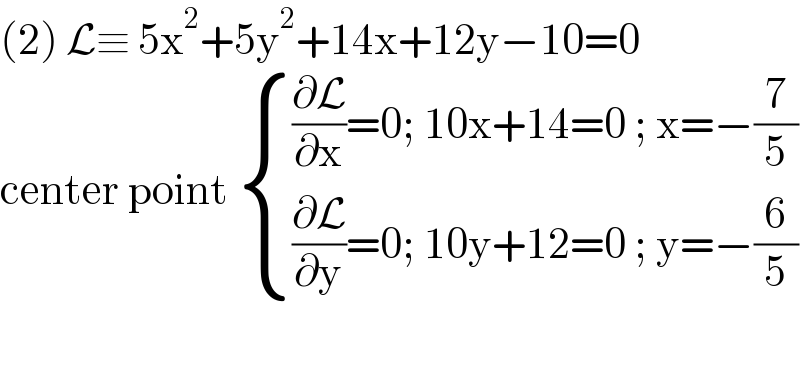
$$\left(\mathrm{2}\right)\:\mathcal{L}\equiv\:\mathrm{5x}^{\mathrm{2}} +\mathrm{5y}^{\mathrm{2}} +\mathrm{14x}+\mathrm{12y}−\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{center}\:\mathrm{point}\:\begin{cases}{\frac{\partial\mathcal{L}}{\partial\mathrm{x}}=\mathrm{0};\:\mathrm{10x}+\mathrm{14}=\mathrm{0}\:;\:\mathrm{x}=−\frac{\mathrm{7}}{\mathrm{5}}}\\{\frac{\partial\mathcal{L}}{\partial\mathrm{y}}=\mathrm{0};\:\mathrm{10y}+\mathrm{12}=\mathrm{0}\:;\:\mathrm{y}=−\frac{\mathrm{6}}{\mathrm{5}}}\end{cases} \\ $$$$ \\ $$
Commented by abdurehime last updated on 17/Jan/21

$$\mathrm{that}\:\:\mathrm{is}\:+ \\ $$
Commented by abdurehime last updated on 17/Jan/21
$$\mathrm{woooooowwww}\:\mathrm{tnks} \\ $$
Answered by liberty last updated on 16/Jan/21
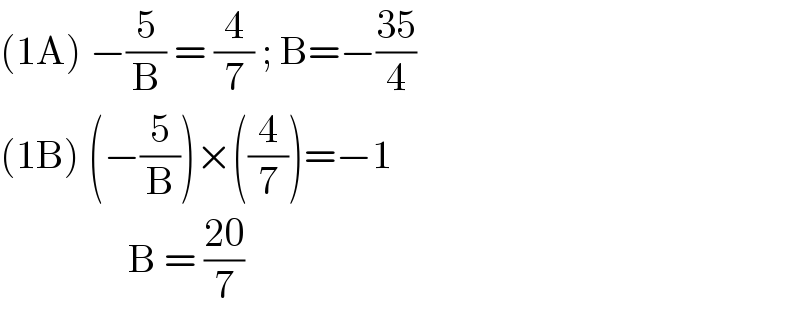
$$\left(\mathrm{1A}\right)\:−\frac{\mathrm{5}}{\mathrm{B}}\:=\:\frac{\mathrm{4}}{\mathrm{7}}\:;\:\mathrm{B}=−\frac{\mathrm{35}}{\mathrm{4}} \\ $$$$\left(\mathrm{1B}\right)\:\left(−\frac{\mathrm{5}}{\mathrm{B}}\right)×\left(\frac{\mathrm{4}}{\mathrm{7}}\right)=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{B}\:=\:\frac{\mathrm{20}}{\mathrm{7}} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Jan/21
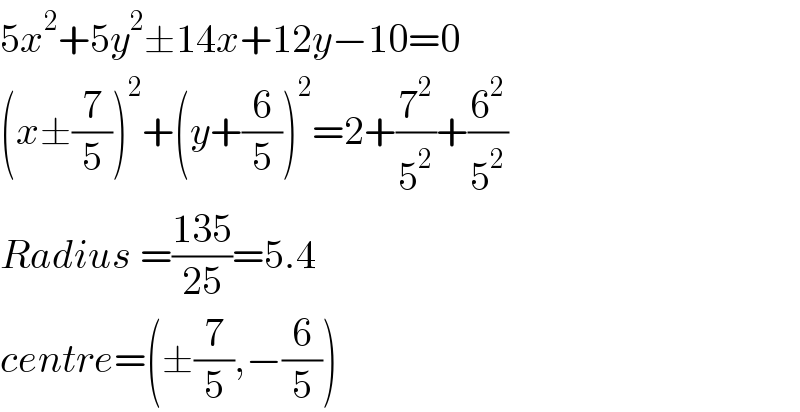
$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{5}{y}^{\mathrm{2}} \pm\mathrm{14}{x}+\mathrm{12}{y}−\mathrm{10}=\mathrm{0} \\ $$$$\left({x}\pm\frac{\mathrm{7}}{\mathrm{5}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{6}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{2}+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} } \\ $$$${Radius}\:=\frac{\mathrm{135}}{\mathrm{25}}=\mathrm{5}.\mathrm{4} \\ $$$${centre}=\left(\pm\frac{\mathrm{7}}{\mathrm{5}},−\frac{\mathrm{6}}{\mathrm{5}}\right) \\ $$
