Question Number 129594 by bagjagunawan last updated on 16/Jan/21
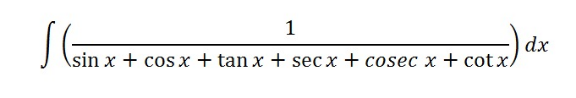
Commented by bemath last updated on 17/Jan/21
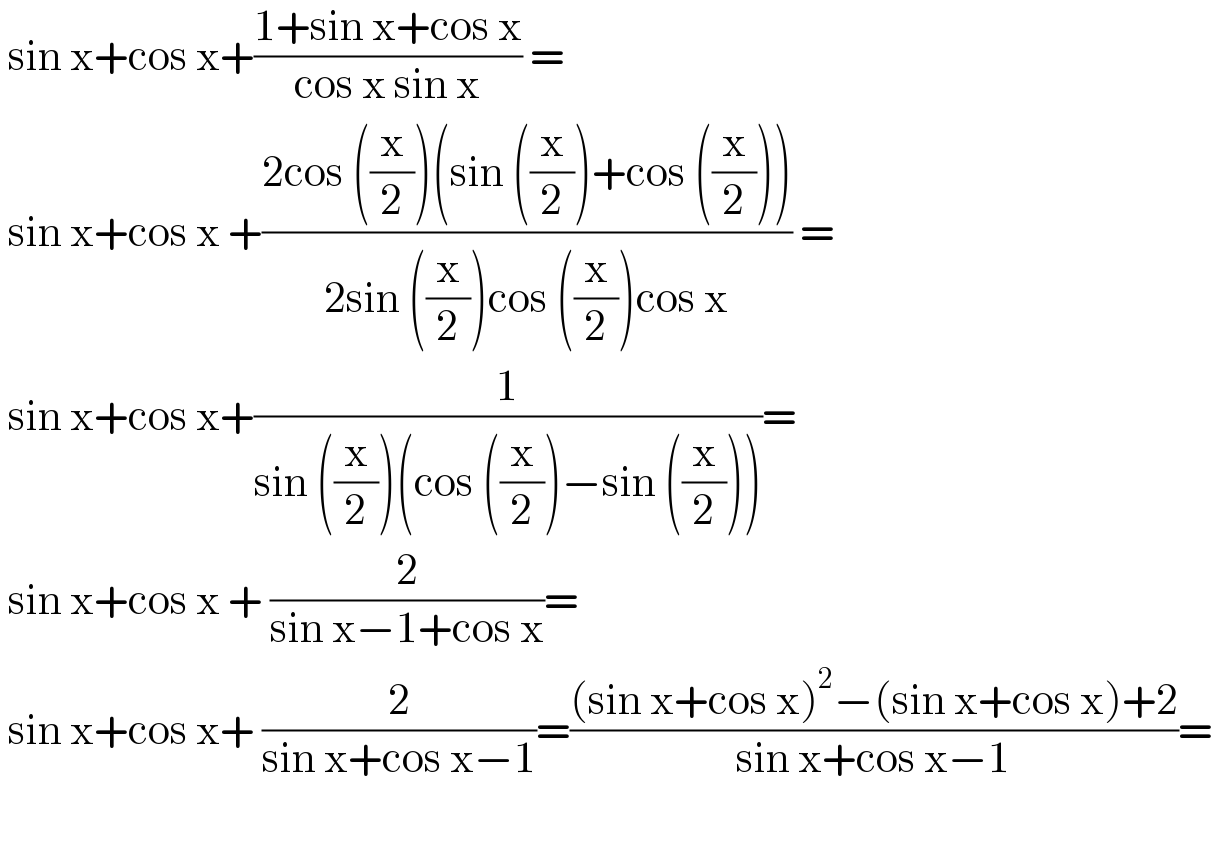
$$\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}\:=\: \\ $$$$\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:+\frac{\mathrm{2cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)}{\mathrm{2sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\:\mathrm{x}}\:= \\ $$$$\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)}= \\ $$$$\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:+\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{x}−\mathrm{1}+\mathrm{cos}\:\mathrm{x}}= \\ $$$$\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}+\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}−\mathrm{1}}=\frac{\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} −\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)+\mathrm{2}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}−\mathrm{1}}= \\ $$$$ \\ $$
