Question Number 129660 by ajfour last updated on 17/Jan/21
Commented by ajfour last updated on 17/Jan/21

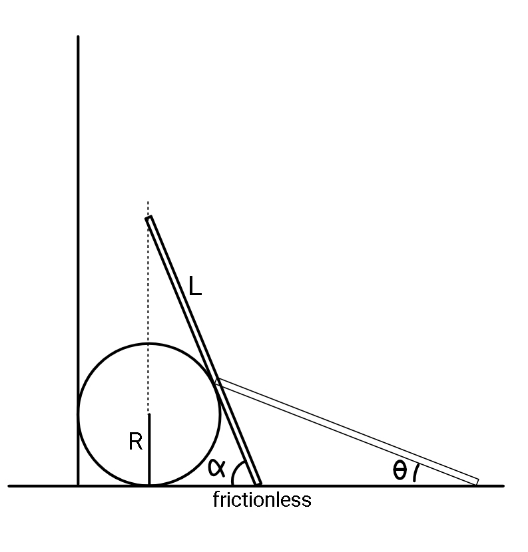
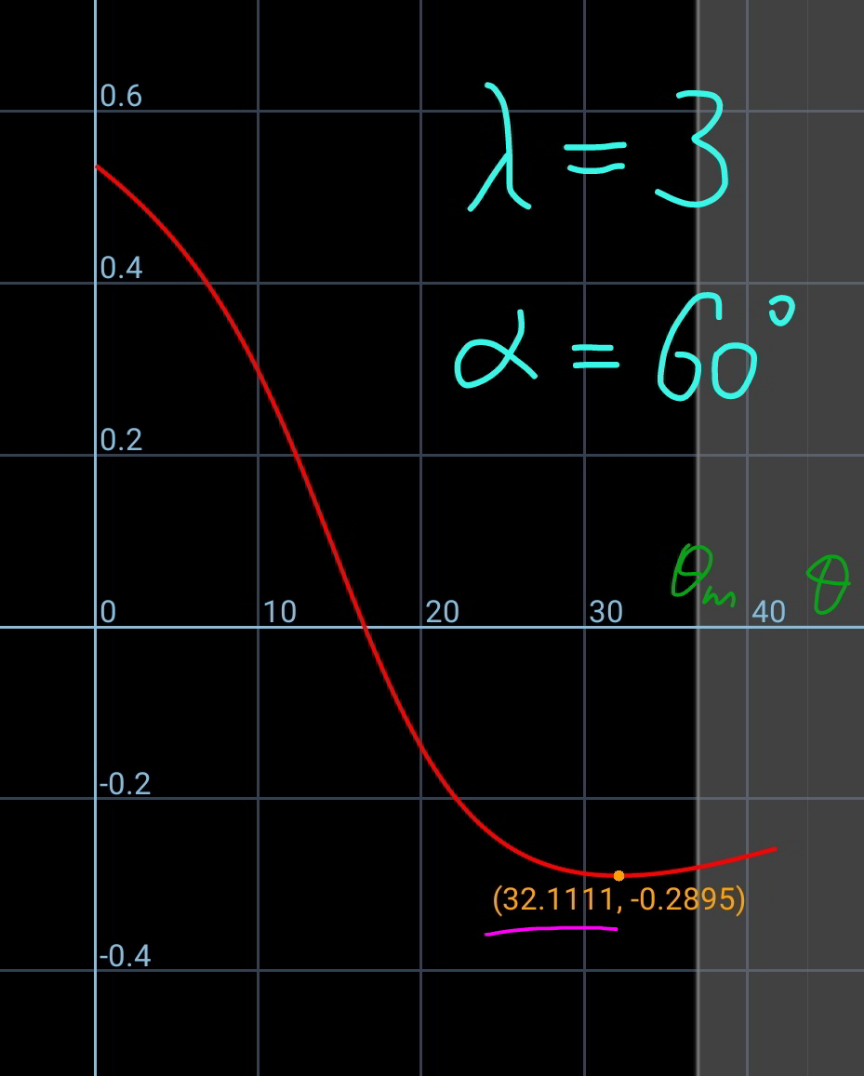
$${If}\:{a}\:{plank}\:{is}\:{released}\:{in}\:{contact} \\ $$$${with}\:{a}\:{smooth}\:{cylinder}\:{of}\:{radius} \\ $$$${R},\:{at}\:{an}\:{angle}\:\alpha.\:{Find}\:{the}\:{angle} \\ $$$$\theta\:{when}\:{plank}\:{is}\:{about}\:{to}\:{leave} \\ $$$${contact}\:{with}\:{cylinder}. \\ $$
Answered by mr W last updated on 18/Jan/21
Commented by mr W last updated on 19/Jan/21
![assumed that the contact point A is the end of the rod when the contact is about to get lost, i.e. θ≤θ_m =2 tan^(−1) (R/L). let λ=(L/R) y_A =R+R cos ϕ=L sin θ ⇒cos ϕ=λ sin θ−1 ⇒sin ϕ=(√(1−(λ sin θ−1)^2 ))=(√(λsin θ(2−λsin θ))) y_C =(L/2) sin θ=R×(λ/2) sin θ x_C =R sin ϕ+(L/2) cos θ=R[(√(λ sin θ(2−λ sin θ)))+(λ/2) cos θ] ω=(dθ/dt) v_(C,x) =(dx_C /dt)=ω(dx_C /dθ)=((ωλR)/2)[((2cos θ(1−λsin θ))/( (√(λ sin θ(2−λ sin θ)))))−sin θ] let η=((cos θ(1−λsin θ))/( (√(λ sin θ(2−λ sin θ))))) ⇒v_(C,x) =((ωλR)/2)(2η−sin θ) v_(C,y) =(dy_C /dt)=ω(dy_C /dθ)=((ωλR)/2)cos θ v_C ^2 =v_(C,x) ^2 +v_(C,y) ^2 =(((ωλR)/2))^2 {(2η−sin θ)^2 +cos^2 θ} ⇒v_C ^2 =(((ωL)/2))^2 [4η(η−sin θ)+1] (1/2)mv_C ^2 +(1/2)(((mL^2 )/(12)))ω^2 =mg(L/2)(sin α−sin θ) v_C ^2 +((L^2 ω^2 )/(12))=gL(sin α−sin θ) ((ω^2 L^2 )/4)[4η(η−sin θ)+1]+((L^2 ω^2 )/(12))=gL(sin α−sin θ) ω^2 [3η(η−sin θ)+1]=((3g)/L)(sin α−sin θ) ⇒ω=(√((3g)/L))×(√((sin α−sin θ)/(3η(η−sin θ)+1))) v_(C,x) =((ωL)/2)(2η−sin θ) a_(C,x) =(dv_(C,x) /dt)=ω(dv_(C,x) /dθ)=ω(d/dθ){((ωL)/2)(2η−sin θ)} N sin ϕ=ma_(C,x) N=0 ⇒ a_(C,x) =0 ⇒(d/dθ){(√((sin α−sin θ)/(3η(η−sin θ)+1)))(η−((sin θ)/2))}=0 that means (√((sin α−sin θ)/(3η(η−sin θ)+1)))(η−((sin θ)/2))=extremal example: λ=(L/R)=3, α=60° ⇒θ≈32.1111° < 2 tan^(−1) (1/3)≈36.87°✓](https://www.tinkutara.com/question/Q129690.png)
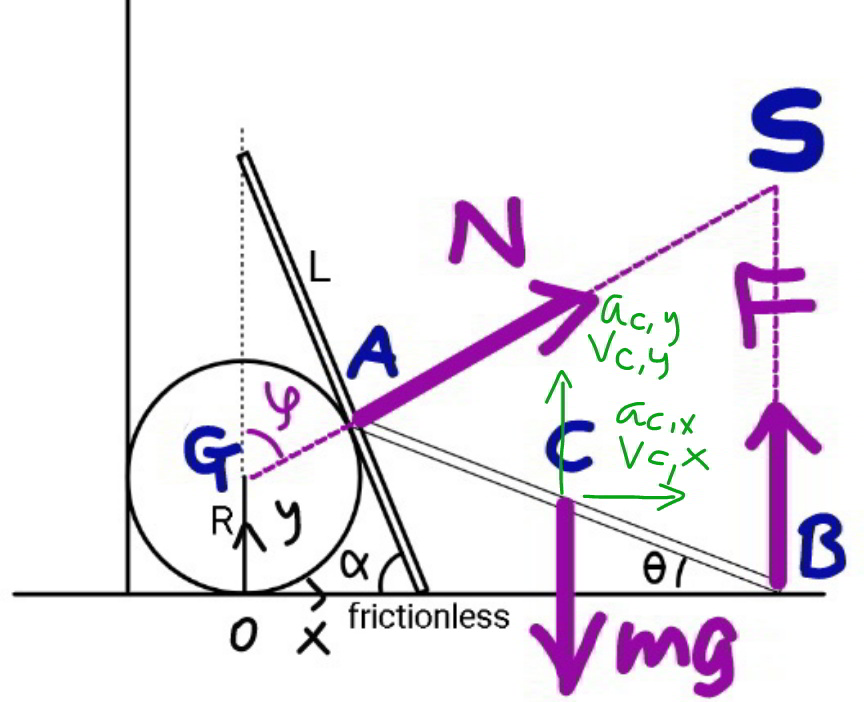
$${assumed}\:{that}\:{the}\:{contact}\:{point}\:{A}\:{is} \\ $$$${the}\:{end}\:{of}\:{the}\:{rod}\:{when}\:{the}\:{contact} \\ $$$${is}\:{about}\:{to}\:{get}\:{lost},\:{i}.{e}.\:\theta\leqslant\theta_{{m}} =\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{{R}}{{L}}. \\ $$$${let}\:\lambda=\frac{{L}}{{R}} \\ $$$${y}_{{A}} ={R}+{R}\:\mathrm{cos}\:\varphi={L}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\varphi=\lambda\:\mathrm{sin}\:\theta−\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\sqrt{\mathrm{1}−\left(\lambda\:\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\lambda\mathrm{sin}\:\theta\left(\mathrm{2}−\lambda\mathrm{sin}\:\theta\right)} \\ $$$${y}_{{C}} =\frac{{L}}{\mathrm{2}}\:\mathrm{sin}\:\theta={R}×\frac{\lambda}{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${x}_{{C}} ={R}\:\mathrm{sin}\:\varphi+\frac{{L}}{\mathrm{2}}\:\mathrm{cos}\:\theta={R}\left[\sqrt{\lambda\:\mathrm{sin}\:\theta\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)}+\frac{\lambda}{\mathrm{2}}\:\mathrm{cos}\:\theta\right] \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${v}_{{C},{x}} =\frac{{dx}_{{C}} }{{dt}}=\omega\frac{{dx}_{{C}} }{{d}\theta}=\frac{\omega\lambda{R}}{\mathrm{2}}\left[\frac{\mathrm{2cos}\:\theta\left(\mathrm{1}−\lambda\mathrm{sin}\:\theta\right)}{\:\sqrt{\lambda\:\mathrm{sin}\:\theta\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)}}−\mathrm{sin}\:\theta\right] \\ $$$${let}\:\eta=\frac{\mathrm{cos}\:\theta\left(\mathrm{1}−\lambda\mathrm{sin}\:\theta\right)}{\:\sqrt{\lambda\:\mathrm{sin}\:\theta\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)}} \\ $$$$\Rightarrow{v}_{{C},{x}} =\frac{\omega\lambda{R}}{\mathrm{2}}\left(\mathrm{2}\eta−\mathrm{sin}\:\theta\right) \\ $$$${v}_{{C},{y}} =\frac{{dy}_{{C}} }{{dt}}=\omega\frac{{dy}_{{C}} }{{d}\theta}=\frac{\omega\lambda{R}}{\mathrm{2}}\mathrm{cos}\:\theta \\ $$$${v}_{{C}} ^{\mathrm{2}} ={v}_{{C},{x}} ^{\mathrm{2}} +{v}_{{C},{y}} ^{\mathrm{2}} =\left(\frac{\omega\lambda{R}}{\mathrm{2}}\right)^{\mathrm{2}} \left\{\left(\mathrm{2}\eta−\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:\theta\right\} \\ $$$$\Rightarrow{v}_{{C}} ^{\mathrm{2}} =\left(\frac{\omega{L}}{\mathrm{2}}\right)^{\mathrm{2}} \left[\mathrm{4}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{C}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}\right)\omega^{\mathrm{2}} ={mg}\frac{{L}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$${v}_{{C}} ^{\mathrm{2}} +\frac{{L}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}}={gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\frac{\omega^{\mathrm{2}} {L}^{\mathrm{2}} }{\mathrm{4}}\left[\mathrm{4}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}\right]+\frac{{L}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}}={gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} \left[\mathrm{3}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}\right]=\frac{\mathrm{3}{g}}{{L}}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{3}{g}}{{L}}}×\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{3}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}}} \\ $$$${v}_{{C},{x}} =\frac{\omega{L}}{\mathrm{2}}\left(\mathrm{2}\eta−\mathrm{sin}\:\theta\right) \\ $$$${a}_{{C},{x}} =\frac{{dv}_{{C},{x}} }{{dt}}=\omega\frac{{dv}_{{C},{x}} }{{d}\theta}=\omega\frac{{d}}{{d}\theta}\left\{\frac{\omega{L}}{\mathrm{2}}\left(\mathrm{2}\eta−\mathrm{sin}\:\theta\right)\right\} \\ $$$${N}\:\mathrm{sin}\:\varphi={ma}_{{C},{x}} \\ $$$${N}=\mathrm{0}\:\Rightarrow\:{a}_{{C},{x}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{d}}{{d}\theta}\left\{\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{3}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}}}\left(\eta−\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\right\}=\mathrm{0} \\ $$$${that}\:{means} \\ $$$$\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{3}\eta\left(\eta−\mathrm{sin}\:\theta\right)+\mathrm{1}}}\left(\eta−\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)={extremal} \\ $$$$ \\ $$$${example}: \\ $$$$\lambda=\frac{{L}}{{R}}=\mathrm{3},\:\alpha=\mathrm{60}° \\ $$$$\Rightarrow\theta\approx\mathrm{32}.\mathrm{1111}°\:<\:\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\approx\mathrm{36}.\mathrm{87}°\checkmark \\ $$
Commented by ajfour last updated on 18/Jan/21
$${Thank}\:{you},\:{Sir},\:{for}\:{the}\:{divine} \\ $$$${light},\:{i}\:{was}\:{in}\:{great}\:{need}\:{of}\:{it}.. \\ $$
Commented by ajfour last updated on 17/Jan/21

$${Thanks}\:{Sir},\:{lets}\:{continue}\: \\ $$$${the}\:{discussion}\:{tomorrow}.. \\ $$
Commented by mr W last updated on 18/Jan/21
Commented by mr W last updated on 18/Jan/21
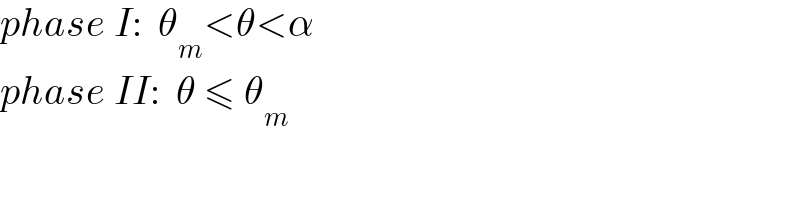
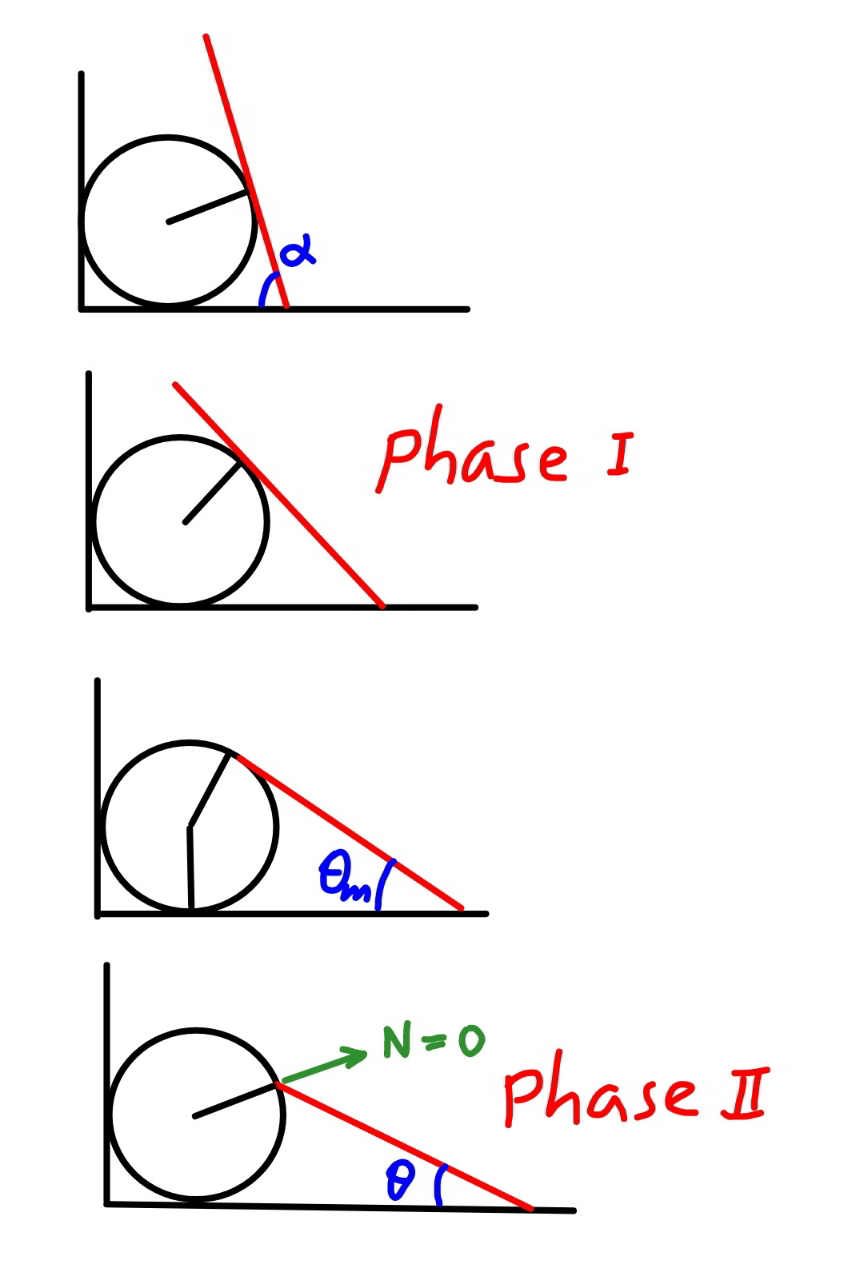
$${phase}\:{I}:\:\:\theta_{{m}} <\theta<\alpha \\ $$$${phase}\:{II}:\:\:\theta\:\leqslant\:\theta_{{m}} \\ $$
Commented by mr W last updated on 18/Jan/21
Answered by mr W last updated on 18/Jan/21
Commented by mr W last updated on 22/Jan/21
![phase I λ=(L/R) θ_m =2 tan^(−1) (1/λ) θ_m <θ<α x_C =(R/(tan (θ/2)))−(L/2)cos θ=R((1/(tan (θ/2)))−((λcos θ)/2)) y_C =(L/2)sin θ=R((λ sin θ)/2) ω=(dθ/dt) v_(C,) x=(dx_C /dt)=ω(dx_C /dθ)=((ωR)/2)(−(1/(sin^2 (θ/2)))+λ sin θ) v_(C,y) =ω(dy_C /dθ)=((ωR)/2)λ cos θ v_C ^2 =((ω^2 R^2 )/4)[(−(1/(sin^2 (θ/2)))+λ sin θ)^2 +λ^2 cos^2 θ] v_C ^2 =((ω^2 R^2 )/4)((1/(sin^4 (θ/2)))−((4λ)/(tan (θ/2)))+λ^2 ) (1/2)mv_C ^2 +(1/2)(((mL^2 )/(12)))ω^2 =mg(L/2)(sin α−sin θ) ((ω^2 R^2 )/4)((1/(sin^4 (θ/2)))−((4λ)/(tan (θ/2)))+λ^2 )+((L^2 /(12)))ω^2 =gL(sin α−sin θ) [(3/(sin^4 (θ/2)))−((12λ)/(tan (θ/2)))+4λ^2 ]ω^2 =((12g)/L)λ^2 (sin α−sin θ) ⇒ω=(√((12g)/L))×(√((sin α−sin θ)/((3/(λ^2 sin^4 (θ/2)))−((12)/(λ tan (θ/2)))+4))) v_(C,x) =((ωR)/2)(−(1/(sin^2 (θ/2)))+λ sin θ) =R(√((3g)/L))×(√((sin α−sin θ)/((3/(λ^2 sin^4 (θ/2)))−((12)/(λ tan (θ/2)))+4)))(−(1/(sin^2 (θ/2)))+λ sin θ) a_(C,x) =ω(dv_(C,x) /dθ) a_(C,x) =ωR(√((3g)/L))× (d/dθ)[(√((sin α−sin θ)/((3/(λ^2 sin^4 (θ/2)))−((12)/(λ tan (θ/2)))+4)))(−(1/(sin^2 (θ/2)))+λ sin θ)] N sin θ=ma_(C,x) N=0 ⇒ a_(C,x) =0 ⇒(d/dθ)[(√((sin α−sin θ)/((3/(λ^2 sin^4 (θ/2)))−((12)/(λ tan (θ/2)))+4)))(−(1/(sin^2 (θ/2)))+λ sin θ)]=0 i.e. (√((sin α−sin θ)/((3/(λ^2 sin^4 (θ/2)))−((12)/(λ tan (θ/2)))+4)))(−(1/(sin^2 (θ/2)))+λ sin θ)=extermal with θ_m <θ<α this has normally no solution, i.e. in phase I we can′t get the case N=0.](https://www.tinkutara.com/question/Q129775.png)
$${phase}\:{I} \\ $$$$\lambda=\frac{{L}}{{R}} \\ $$$$\theta_{{m}} =\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\lambda} \\ $$$$\theta_{{m}} <\theta<\alpha \\ $$$${x}_{{C}} =\frac{{R}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\theta={R}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\frac{\lambda\mathrm{cos}\:\theta}{\mathrm{2}}\right) \\ $$$${y}_{{C}} =\frac{{L}}{\mathrm{2}}\mathrm{sin}\:\theta={R}\frac{\lambda\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${v}_{{C},} {x}=\frac{{dx}_{{C}} }{{dt}}=\omega\frac{{dx}_{{C}} }{{d}\theta}=\frac{\omega{R}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right) \\ $$$${v}_{{C},{y}} =\omega\frac{{dy}_{{C}} }{{d}\theta}=\frac{\omega{R}}{\mathrm{2}}\lambda\:\mathrm{cos}\:\theta \\ $$$${v}_{{C}} ^{\mathrm{2}} =\frac{\omega^{\mathrm{2}} {R}^{\mathrm{2}} }{\mathrm{4}}\left[\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\right] \\ $$$${v}_{{C}} ^{\mathrm{2}} =\frac{\omega^{\mathrm{2}} {R}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{4}\lambda}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\lambda^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{C}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}\right)\omega^{\mathrm{2}} ={mg}\frac{{L}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\frac{\omega^{\mathrm{2}} {R}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{4}\lambda}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\lambda^{\mathrm{2}} \right)+\left(\frac{{L}^{\mathrm{2}} }{\mathrm{12}}\right)\omega^{\mathrm{2}} ={gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\left[\frac{\mathrm{3}}{\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}\lambda}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}\lambda^{\mathrm{2}} \right]\omega^{\mathrm{2}} =\frac{\mathrm{12}{g}}{{L}}\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{12}{g}}{{L}}}×\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}}{\lambda\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}}} \\ $$$${v}_{{C},{x}} =\frac{\omega{R}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:={R}\sqrt{\frac{\mathrm{3}{g}}{{L}}}×\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}}{\lambda\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right) \\ $$$${a}_{{C},{x}} =\omega\frac{{dv}_{{C},{x}} }{{d}\theta} \\ $$$${a}_{{C},{x}} =\omega{R}\sqrt{\frac{\mathrm{3}{g}}{{L}}}×\:\frac{{d}}{{d}\theta}\left[\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}}{\lambda\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right)\right] \\ $$$${N}\:\mathrm{sin}\:\theta={ma}_{{C},{x}} \\ $$$${N}=\mathrm{0}\:\Rightarrow\:{a}_{{C},{x}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{d}}{{d}\theta}\left[\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}}{\lambda\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right)\right]=\mathrm{0} \\ $$$${i}.{e}. \\ $$$$\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{12}}{\lambda\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}}}\left(−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}+\lambda\:\mathrm{sin}\:\theta\right)={extermal} \\ $$$${with}\:\theta_{{m}} <\theta<\alpha \\ $$$${this}\:{has}\:{normally}\:{no}\:{solution},\:{i}.{e}. \\ $$$${in}\:{phase}\:{I}\:{we}\:{can}'{t}\:{get}\:{the}\:{case}\:{N}=\mathrm{0}. \\ $$
Commented by mr W last updated on 19/Jan/21

Answered by mr W last updated on 19/Jan/21
Commented by mr W last updated on 20/Jan/21
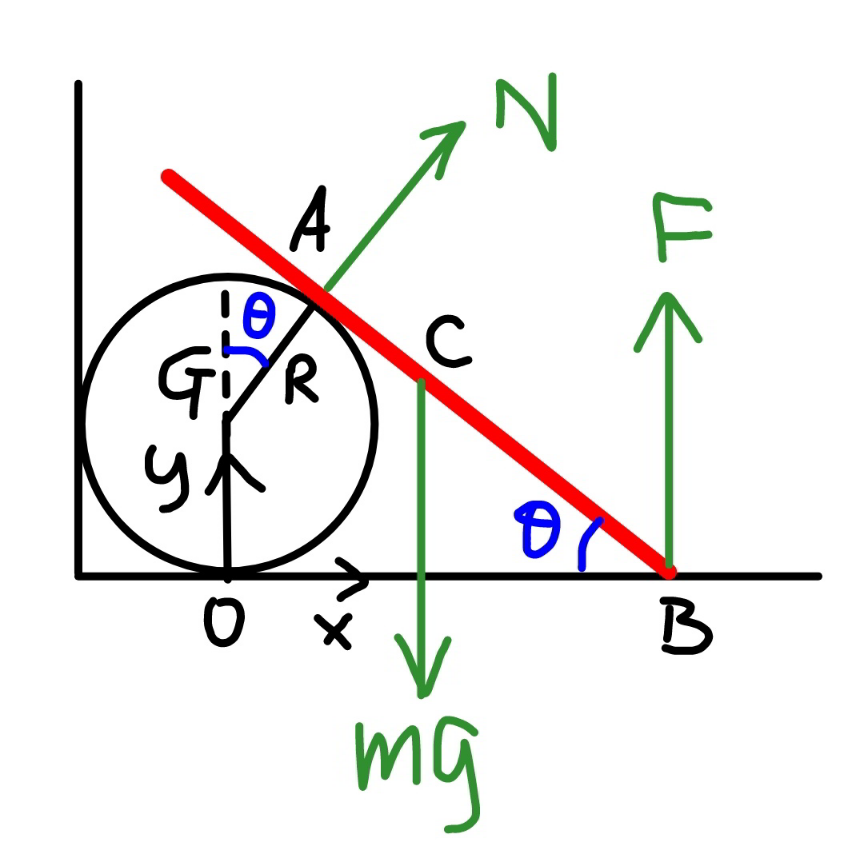
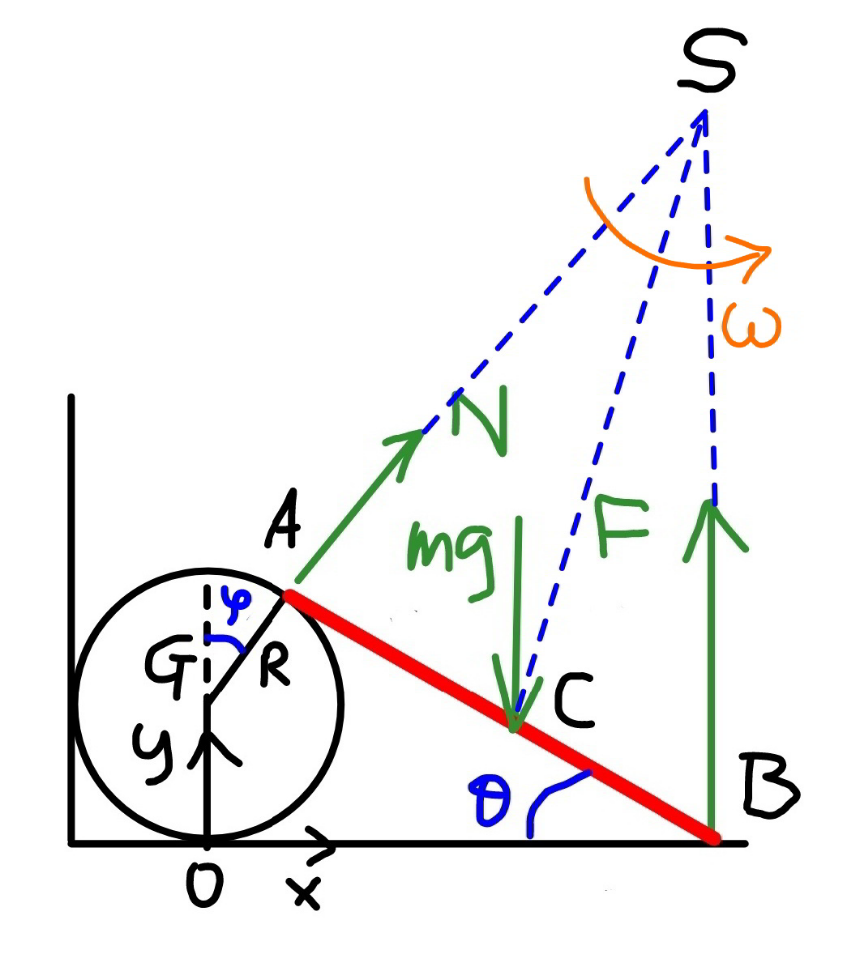
![Phase II − an other way R(1+cos ϕ)=L sin θ cos ϕ=((L sin θ)/R)−1=λ sin θ−1 tan ϕ=((√(λ sin θ (2−λ sin θ)))/(λ sin θ−1)) SB=R+((OB)/(tan ϕ))=R+((L cos θ+R sin ϕ)/(tan ϕ)) SB=(1+cos ϕ+((λ cos θ)/(tan ϕ)))R ⇒SB=L(sin θ+((cos θ)/(tan ϕ))) SC^2 =((L/2))^2 +L^2 (sin θ+((cos θ)/(tan ϕ)))^2 −2×(L/2)×L(sin θ+((cos θ)/(tan ϕ)))×cos ((π/2)−θ) SC^2 =L^2 [(1/4)+(sin θ+((cos θ)/(tan ϕ)))^2 −sin θ (sin θ+((cos θ)/(tan ϕ)))] ⇒SC^2 =[(1/4)+((cos θ)/(tan ϕ))(sin θ+((cos θ)/(tan ϕ)))]L^2 I_S =I+m×SC^2 =((mL^2 )/(12))+[(1/4)+((cos θ)/(tan ϕ))(sin θ+((cos θ)/(tan ϕ)))]mL^2 ⇒I_S =[(1/3)+((cos θ)/(tan ϕ))(sin θ+((cos θ)/(tan ϕ)))]mL^2 ω=(dθ/dt) (1/2)I_S ω^2 =mg(L/2)(sin α−sin θ) [(1/3)+((cos θ)/(tan ϕ))(sin θ+((cos θ)/(tan ϕ)))]mL^2 ω^2 =mgL(sin α−sin θ) ⇒ω^2 =((3g)/L)×((sin α−sin θ)/(1+((3 cos θ)/(tan ϕ))(sin θ+((cos θ)/(tan ϕ))))) let ξ=((cos θ)/(tan ϕ))=((cos θ (λ sin θ−1))/( (√(λ sin θ (2−λ sin θ))))) ⇒ω=(√((3g)/L))×(√((sin α−sin θ)/(1+3ξ(sin θ+ξ)))) v_(C,x) =ω(SB−(L/2)sin θ) ⇒v_(C,x) =ω(((cos θ)/(tan ϕ))+((sin θ)/2))L=ω(ξ+((sin θ)/2))L a_(C,x) =ω(dv_(C,x) /dθ)=ω(√(3gL))×(d/dθ){(ξ+((sin θ)/2))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))} N sin ϕ=ma_(C,x) =mω(√(3gL))×(d/dθ){(ξ+((sin θ)/2))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))} (N/(mg))=(3/(sin ϕ))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))×(d/dθ){(ξ+((sin θ)/2))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))} ⇒(N/(mg))=3(√((sin α−sin θ)/(λ sin θ (2−λ sin θ)[1+3ξ(sin θ+ξ)])))×(d/dθ){(ξ+((sin θ)/2))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))} for N=0 ⇒ a_(C,x) =0 ⇒(d/dθ){(ξ+((sin θ)/2))(√((sin α−sin θ)/(1+3ξ(sin θ+ξ))))}=0](https://www.tinkutara.com/question/Q129830.png)
$$\boldsymbol{{Phase}}\:\boldsymbol{{II}}\:−\:\boldsymbol{{an}}\:\boldsymbol{{other}}\:\boldsymbol{{way}} \\ $$$$ \\ $$$${R}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)={L}\:\mathrm{sin}\:\theta \\ $$$$\mathrm{cos}\:\varphi=\frac{{L}\:\mathrm{sin}\:\theta}{{R}}−\mathrm{1}=\lambda\:\mathrm{sin}\:\theta−\mathrm{1} \\ $$$$\mathrm{tan}\:\varphi=\frac{\sqrt{\lambda\:\mathrm{sin}\:\theta\:\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)}}{\lambda\:\mathrm{sin}\:\theta−\mathrm{1}} \\ $$$${SB}={R}+\frac{{OB}}{\mathrm{tan}\:\varphi}={R}+\frac{{L}\:\mathrm{cos}\:\theta+{R}\:\mathrm{sin}\:\varphi}{\mathrm{tan}\:\varphi} \\ $$$${SB}=\left(\mathrm{1}+\mathrm{cos}\:\varphi+\frac{\lambda\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right){R} \\ $$$$\Rightarrow{SB}={L}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right) \\ $$$${SC}^{\mathrm{2}} =\left(\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} +{L}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)^{\mathrm{2}} −\mathrm{2}×\frac{{L}}{\mathrm{2}}×{L}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)×\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$${SC}^{\mathrm{2}} ={L}^{\mathrm{2}} \left[\frac{\mathrm{1}}{\mathrm{4}}+\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)^{\mathrm{2}} −\mathrm{sin}\:\theta\:\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)\right] \\ $$$$\Rightarrow{SC}^{\mathrm{2}} =\left[\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)\right]{L}^{\mathrm{2}} \\ $$$${I}_{{S}} ={I}+{m}×{SC}^{\mathrm{2}} =\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}+\left[\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)\right]{mL}^{\mathrm{2}} \\ $$$$\Rightarrow{I}_{{S}} =\left[\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)\right]{mL}^{\mathrm{2}} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}_{{S}} \omega^{\mathrm{2}} ={mg}\frac{{L}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)\right]{mL}^{\mathrm{2}} \omega^{\mathrm{2}} ={mgL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{3}{g}}{{L}}×\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\frac{\mathrm{3}\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}\right)} \\ $$$${let}\:\xi=\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}=\frac{\mathrm{cos}\:\theta\:\left(\lambda\:\mathrm{sin}\:\theta−\mathrm{1}\right)}{\:\sqrt{\lambda\:\mathrm{sin}\:\theta\:\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)}}\: \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{3}{g}}{{L}}}×\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}} \\ $$$${v}_{{C},{x}} =\omega\left({SB}−\frac{{L}}{\mathrm{2}}\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{v}_{{C},{x}} =\omega\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right){L}=\omega\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right){L} \\ $$$${a}_{{C},{x}} =\omega\frac{{dv}_{{C},{x}} }{{d}\theta}=\omega\sqrt{\mathrm{3}{gL}}×\frac{{d}}{{d}\theta}\left\{\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}\right\} \\ $$$${N}\:\mathrm{sin}\:\varphi={ma}_{{C},{x}} ={m}\omega\sqrt{\mathrm{3}{gL}}×\frac{{d}}{{d}\theta}\left\{\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}\right\} \\ $$$$\frac{{N}}{{mg}}=\frac{\mathrm{3}}{\mathrm{sin}\:\varphi}\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}×\frac{{d}}{{d}\theta}\left\{\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}\right\} \\ $$$$\Rightarrow\frac{{N}}{{mg}}=\mathrm{3}\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\lambda\:\mathrm{sin}\:\theta\:\left(\mathrm{2}−\lambda\:\mathrm{sin}\:\theta\right)\left[\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)\right]}}×\frac{{d}}{{d}\theta}\left\{\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}\right\} \\ $$$$ \\ $$$${for}\:{N}=\mathrm{0}\:\Rightarrow\:{a}_{{C},{x}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{d}}{{d}\theta}\left\{\left(\xi+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\xi\left(\mathrm{sin}\:\theta+\xi\right)}}\right\}=\mathrm{0} \\ $$
Commented by ajfour last updated on 23/Jan/21

$${Reviewing}\:{these}\:{solutions},\:{Sir}. \\ $$$${Thank}\:{you}\:{plentifully}! \\ $$
Commented by mr W last updated on 21/Jan/21
$${best}\:{wish}\:{for}\:{your}\:{health}\:{sir}! \\ $$
