Question Number 129795 by ajfour last updated on 19/Jan/21
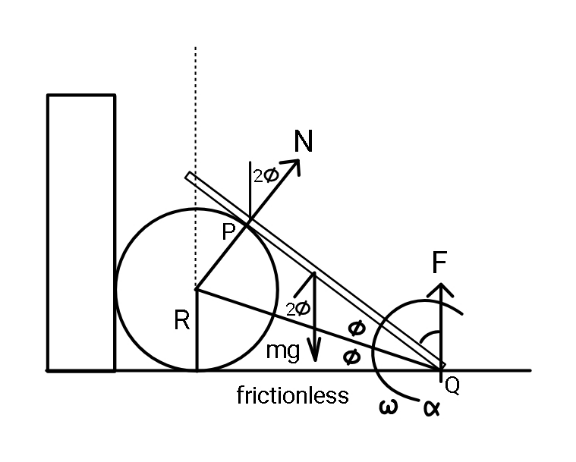
Commented by ajfour last updated on 19/Jan/21
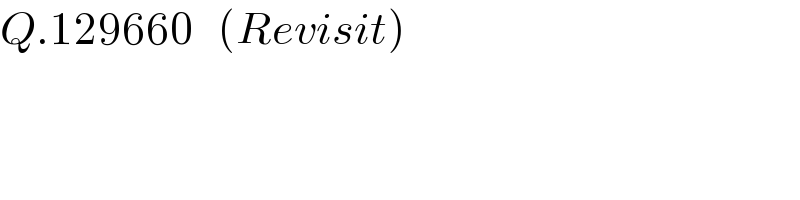
$${Q}.\mathrm{129660}\:\:\:\left({Revisit}\right) \\ $$
Answered by ajfour last updated on 23/Jan/21
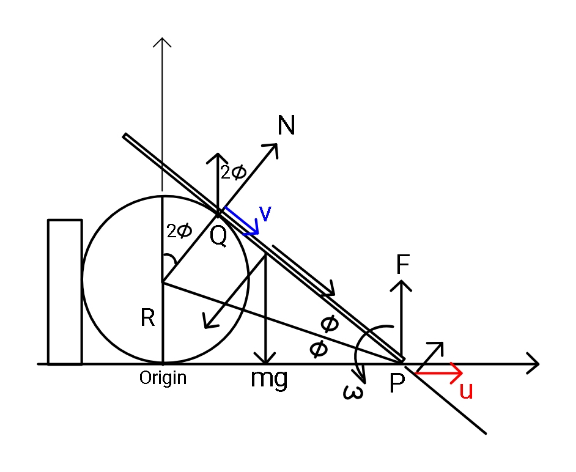
Commented by ajfour last updated on 23/Jan/21
![From work-energy balance mg((L/2))[sin 2φ_0 −sin 2φ] =(1/2)m(v_(cm) ^2 )+(1/2)I_(cm) ω^2 ucos 2φ−v=−Rcosec^2 φ((dφ/dt)) OP =p=Rcot φ (dp/dt)=−(Rcosec^2 φ)(dφ/dt)=u ⇒ (dφ/dt)=−(u/R)sin^2 φ usin 2φ=ωRcot φ v_(cm) ^2 =v_(x,cm) ^2 +v_(y,cm) ^2 v_x =(d/dt)(Rcot φ−(L/2)cos 2φ) v_y =(d/dt)((L/2)sin 2φ) v_(cm) ^2 =(Lsin 2φ−Rcosec^2 φ)^2 ((dφ/dt))^2 +(Lcos 2φ)^2 ((dφ/dt))^2 ω=((usin 2φ)/(Rcot φ))=−(((cosec^2 φsin 2φ)/(cot φ)))(dφ/dt) −−−−−−−−−−−−−−− gL(sin 2φ_0 −sin 2φ) =((dφ/dt))^2 [(I_(cm) /m)(((cosec^2 φsin 2φ)/(cot φ)))^2 +(Lsin 2φ−Rcosec^2 φ)^2 +(Lcos 2φ)^2 ] ⇒ ((dφ/dt))^2 =((gL(sin 2φ_0 −sin 2φ))/((I_(cm) /m)(((cosec^2 φsin 2φ)/(cot φ)))^2 +(Lsin 2φ−Rcosec^2 φ)^2 +(Lcos 2φ)^2 )) ω^2 =((4gL(sin 2φ_0 −sin 2φ_1 ))/(((4L^2 )/3)+R^2 cosec^4 φ−4RLcot φ)) ω^2 =((12gλ(sin α−sin θ))/(R(4λ^2 +3cosec^4 (θ/2)−12λcot (θ/2)))) say φ=φ_1 =tan^(−1) ((R/L)) Now phase II starts: ...............................](https://www.tinkutara.com/question/Q130237.png)
$${From}\:{work}-{energy}\:{balance} \\ $$$${mg}\left(\frac{{L}}{\mathrm{2}}\right)\left[\mathrm{sin}\:\mathrm{2}\phi_{\mathrm{0}} −\mathrm{sin}\:\mathrm{2}\phi\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{m}\left({v}_{{cm}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}{I}_{{cm}} \omega^{\mathrm{2}} \\ $$$${u}\mathrm{cos}\:\mathrm{2}\phi−{v}=−{R}\mathrm{cosec}\:^{\mathrm{2}} \phi\left(\frac{{d}\phi}{{dt}}\right) \\ $$$${OP}\:={p}={R}\mathrm{cot}\:\phi \\ $$$$\frac{{dp}}{{dt}}=−\left({R}\mathrm{cosec}\:^{\mathrm{2}} \phi\right)\frac{{d}\phi}{{dt}}={u} \\ $$$$\Rightarrow\:\:\frac{{d}\phi}{{dt}}=−\frac{{u}}{{R}}\mathrm{sin}\:^{\mathrm{2}} \phi \\ $$$${u}\mathrm{sin}\:\mathrm{2}\phi=\omega{R}\mathrm{cot}\:\phi \\ $$$${v}_{{cm}} ^{\mathrm{2}} ={v}_{{x},{cm}} ^{\mathrm{2}} +{v}_{{y},{cm}} ^{\mathrm{2}} \\ $$$$\:{v}_{{x}} =\frac{{d}}{{dt}}\left({R}\mathrm{cot}\:\phi−\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\phi\right) \\ $$$$\:{v}_{{y}} =\frac{{d}}{{dt}}\left(\frac{{L}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\phi\right) \\ $$$${v}_{{cm}} ^{\mathrm{2}} =\left({L}\mathrm{sin}\:\mathrm{2}\phi−{R}\mathrm{cosec}\:^{\mathrm{2}} \phi\right)^{\mathrm{2}} \left(\frac{{d}\phi}{{dt}}\right)^{\mathrm{2}} \\ $$$$\:\:+\left({L}\mathrm{cos}\:\mathrm{2}\phi\right)^{\mathrm{2}} \left(\frac{{d}\phi}{{dt}}\right)^{\mathrm{2}} \\ $$$$\omega=\frac{{u}\mathrm{sin}\:\mathrm{2}\phi}{{R}\mathrm{cot}\:\phi}=−\left(\frac{\mathrm{cosec}\:^{\mathrm{2}} \phi\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{cot}\:\phi}\right)\frac{{d}\phi}{{dt}} \\ $$$$−−−−−−−−−−−−−−− \\ $$$${gL}\left(\mathrm{sin}\:\mathrm{2}\phi_{\mathrm{0}} −\mathrm{sin}\:\mathrm{2}\phi\right) \\ $$$$=\left(\frac{{d}\phi}{{dt}}\right)^{\mathrm{2}} \left[\frac{{I}_{{cm}} }{{m}}\left(\frac{\mathrm{cosec}\:^{\mathrm{2}} \phi\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{cot}\:\phi}\right)^{\mathrm{2}} \right. \\ $$$$\:\:\:+\left({L}\mathrm{sin}\:\mathrm{2}\phi−{R}\mathrm{cosec}\:^{\mathrm{2}} \phi\right)^{\mathrm{2}} \\ $$$$\left.\:\:+\left({L}\mathrm{cos}\:\mathrm{2}\phi\right)^{\mathrm{2}} \right] \\ $$$$\Rightarrow \\ $$$$\left(\frac{{d}\phi}{{dt}}\right)^{\mathrm{2}} =\frac{{gL}\left(\mathrm{sin}\:\mathrm{2}\phi_{\mathrm{0}} −\mathrm{sin}\:\mathrm{2}\phi\right)}{\frac{{I}_{{cm}} }{{m}}\left(\frac{\mathrm{cosec}\:^{\mathrm{2}} \phi\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{cot}\:\phi}\right)^{\mathrm{2}} +\left({L}\mathrm{sin}\:\mathrm{2}\phi−{R}\mathrm{cosec}\:^{\mathrm{2}} \phi\right)^{\mathrm{2}} +\left({L}\mathrm{cos}\:\mathrm{2}\phi\right)^{\mathrm{2}} } \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{4}{gL}\left(\mathrm{sin}\:\mathrm{2}\phi_{\mathrm{0}} −\mathrm{sin}\:\mathrm{2}\phi_{\mathrm{1}} \right)}{\frac{\mathrm{4}{L}^{\mathrm{2}} }{\mathrm{3}}+{R}^{\mathrm{2}} \mathrm{cosec}\:^{\mathrm{4}} \phi−\mathrm{4}{RL}\mathrm{cot}\:\phi} \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{12}{g}\lambda\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right)}{{R}\left(\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{3cosec}\:^{\mathrm{4}} \frac{\theta}{\mathrm{2}}−\mathrm{12}\lambda\mathrm{cot}\:\frac{\theta}{\mathrm{2}}\right)} \\ $$$${say}\:\:\:\phi=\phi_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{R}}{{L}}\right) \\ $$$${Now}\:{phase}\:{II}\:{starts}: \\ $$$$…………………………. \\ $$
