Question Number 129903 by 0731619177 last updated on 20/Jan/21
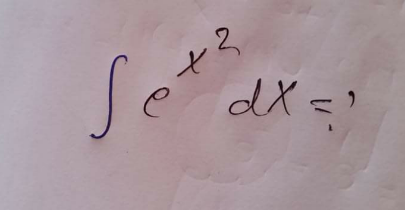
Commented by Dwaipayan Shikari last updated on 20/Jan/21

$$\int{e}^{{x}^{\mathrm{2}} } {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}{x}^{\mathrm{2}{n}+\mathrm{1}} =\frac{{x}}{\mathrm{1}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{10}}+\frac{{x}^{\mathrm{7}} }{\mathrm{42}}+\frac{{x}^{\mathrm{9}} }{\mathrm{216}}+…+{C} \\ $$$$=\frac{{x}}{\mathrm{1}−\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{10}}}{\mathrm{1}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{10}}−\frac{\frac{\mathrm{21}}{\mathrm{5}}{x}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{21}}{\mathrm{5}}{x}^{\mathrm{2}} −..}}}}+{C} \\ $$$$=\frac{{x}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}+{x}^{\mathrm{2}} −\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{10}+\mathrm{3}{x}^{\mathrm{2}} −\frac{\mathrm{21}{x}^{\mathrm{2}} }{\mathrm{5}+\mathrm{21}{x}^{\mathrm{2}} −..}}}}+{C} \\ $$
