Question-129908

Question Number 129908 by Adel last updated on 20/Jan/21

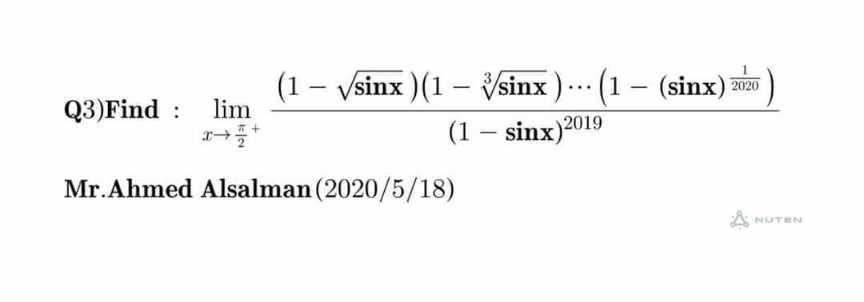
Answered by mathmax by abdo last updated on 20/Jan/21

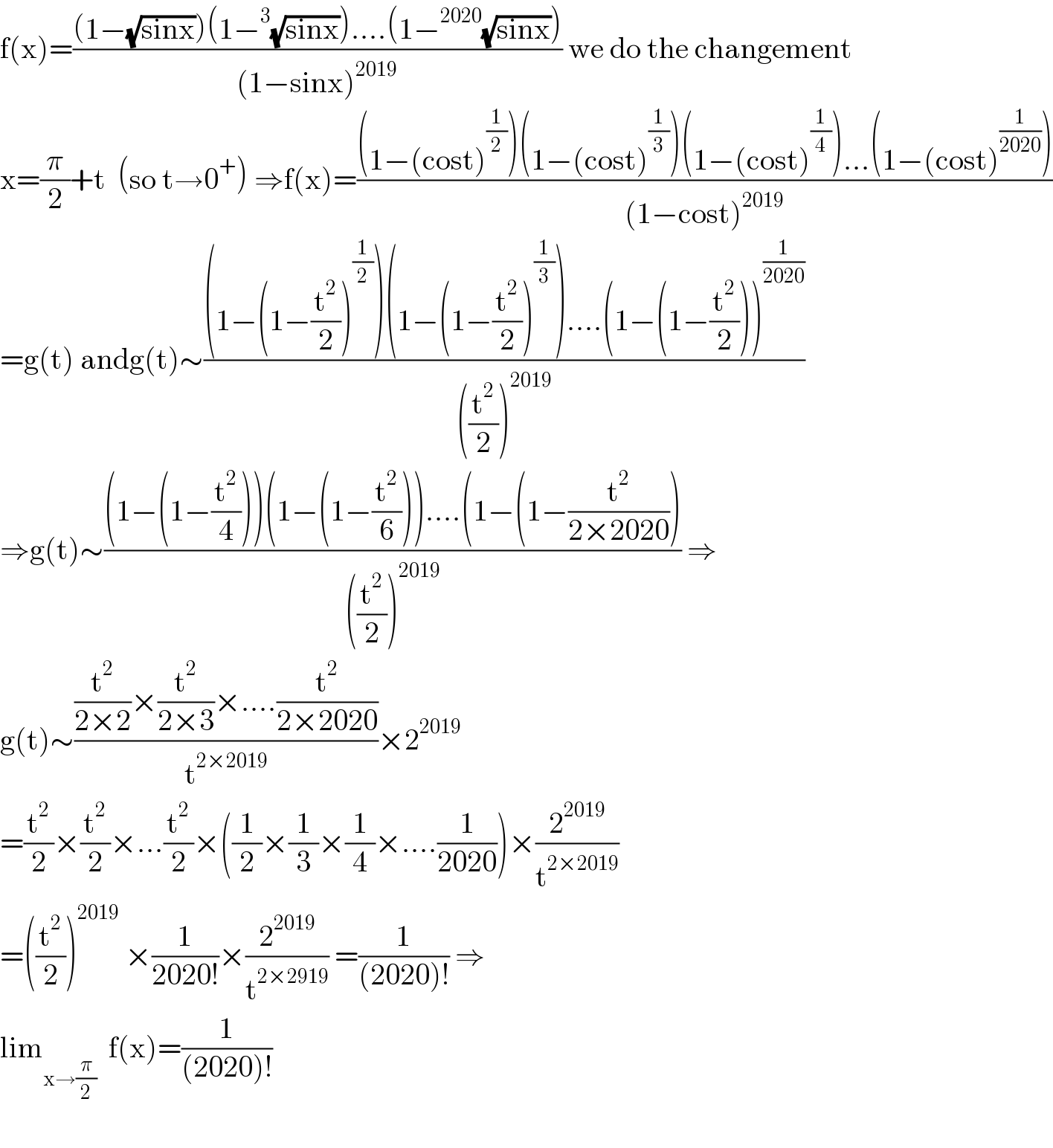
f(x)=(((1−(√(sinx)))(1−^3 (√(sinx)))....(1−^(2020) (√(sinx))))/((1−sinx)^(2019) )) we do the changement x=(π/2)+t (so t→0^+ ) ⇒f(x)=(((1−(cost)^(1/2) )(1−(cost)^(1/3) )(1−(cost)^(1/4) )...(1−(cost)^(1/(2020)) ))/((1−cost)^(2019) )) =g(t) andg(t)∼(((1−(1−(t^2 /2))^(1/2) )(1−(1−(t^2 /2))^(1/3) )....(1−(1−(t^2 /2)))^(1/(2020)) )/(((t^2 /2))^(2019) )) ⇒g(t)∼(((1−(1−(t^2 /4)))(1−(1−(t^2 /6)))....(1−(1−(t^2 /(2×2020))))/(((t^2 /2))^(2019) )) ⇒ g(t)∼(((t^2 /(2×2))×(t^2 /(2×3))×....(t^2 /(2×2020)))/t^(2×2019) )×2^(2019) =(t^2 /2)×(t^2 /2)×...(t^2 /2)×((1/2)×(1/3)×(1/4)×....(1/(2020)))×(2^(2019) /t^(2×2019) ) =((t^2 /2))^(2019) ×(1/(2020!))×(2^(2019) /t^(2×2919) ) =(1/((2020)!)) ⇒ lim_(x→(π/2)) f(x)=(1/((2020)!))

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{1}−\sqrt{\mathrm{sinx}}\right)\left(\mathrm{1}−^{\mathrm{3}} \sqrt{\mathrm{sinx}}\right)….\left(\mathrm{1}−^{\mathrm{2020}} \sqrt{\mathrm{sinx}}\right)}{\left(\mathrm{1}−\mathrm{sinx}\right)^{\mathrm{2019}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{t}\:\:\left(\mathrm{so}\:\mathrm{t}\rightarrow\mathrm{0}^{+} \right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{1}−\left(\mathrm{cost}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\left(\mathrm{1}−\left(\mathrm{cost}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right)\left(\mathrm{1}−\left(\mathrm{cost}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right)…\left(\mathrm{1}−\left(\mathrm{cost}\right)^{\frac{\mathrm{1}}{\mathrm{2020}}} \right)}{\left(\mathrm{1}−\mathrm{cost}\right)^{\mathrm{2019}} } \\ $$$$=\mathrm{g}\left(\mathrm{t}\right)\:\mathrm{andg}\left(\mathrm{t}\right)\sim\frac{\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right)….\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2020}}} }{\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2019}} } \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}\right)\right)\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{6}}\right)\right)….\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2020}}\right)\right.}{\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2019}} }\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}}×\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}}×….\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2020}}}{\mathrm{t}^{\mathrm{2}×\mathrm{2019}} }×\mathrm{2}^{\mathrm{2019}} \\ $$$$=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}×…\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}×….\frac{\mathrm{1}}{\mathrm{2020}}\right)×\frac{\mathrm{2}^{\mathrm{2019}} }{\mathrm{t}^{\mathrm{2}×\mathrm{2019}} } \\ $$$$=\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2019}} \:×\frac{\mathrm{1}}{\mathrm{2020}!}×\frac{\mathrm{2}^{\mathrm{2019}} }{\mathrm{t}^{\mathrm{2}×\mathrm{2919}} }\:=\frac{\mathrm{1}}{\left(\mathrm{2020}\right)!}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{2020}\right)!}\:\: \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply