Question Number 129914 by MrJoe last updated on 20/Jan/21
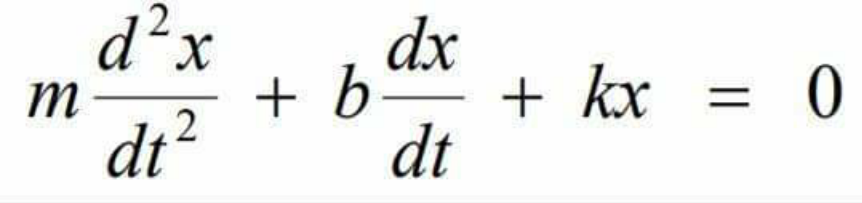
Commented by MrJoe last updated on 20/Jan/21
Find x(t)
Answered by Dwaipayan Shikari last updated on 20/Jan/21
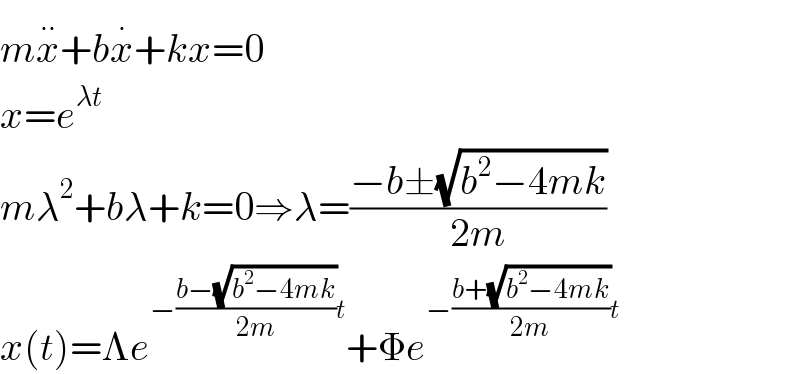
$${m}\overset{..} {{x}}+{b}\overset{.} {{x}}+{kx}=\mathrm{0} \\ $$$${x}={e}^{\lambda{t}} \\ $$$${m}\lambda^{\mathrm{2}} +{b}\lambda+{k}=\mathrm{0}\Rightarrow\lambda=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{mk}}}{\mathrm{2}{m}} \\ $$$${x}\left({t}\right)=\Lambda{e}^{−\frac{{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{mk}}}{\mathrm{2}{m}}{t}} +\Phi{e}^{−\frac{{b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{mk}}}{\mathrm{2}{m}}{t}} \\ $$
