Question Number 129951 by Algoritm last updated on 21/Jan/21

Commented by MJS_new last updated on 21/Jan/21

$$\mathrm{2}^{{x}/\mathrm{3}} −\mathrm{2}^{{x}} =\mathrm{2} \\ $$$${t}=\mathrm{2}^{{x}/\mathrm{3}} \\ $$$${t}−{t}^{\mathrm{3}} =\mathrm{2} \\ $$$${t}\approx−\mathrm{1}.\mathrm{52}\vee{t}\approx.\mathrm{761}\pm.\mathrm{858i} \\ $$$$ \\ $$$$\mathrm{2}^{\mathrm{2}{x}/\mathrm{3}} +\mathrm{2}^{\mathrm{4}{x}/\mathrm{3}} +\mathrm{4}^{{x}} =\mathrm{5} \\ $$$${t}=\mathrm{2}^{{x}/\mathrm{3}} \\ $$$${t}^{\mathrm{6}} +{t}^{\mathrm{4}} +{t}^{\mathrm{2}} =\mathrm{5} \\ $$$${t}\approx\pm\mathrm{1}.\mathrm{13}\vee{t}\approx\pm\left(.\mathrm{648}\pm\mathrm{1}.\mathrm{25i}\right) \\ $$$$ \\ $$$$\mathrm{2}^{{x}} −\mathrm{8}^{{x}} =\mathrm{10}\:\left(?\right) \\ $$$${t}=\mathrm{2}^{{x}/\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{9}} =\mathrm{10} \\ $$$${t}\approx−\mathrm{1}.\mathrm{32}\vee{t}\approx−.\mathrm{960}\pm.\mathrm{841}\vee{t}\approx−.\mathrm{249}\pm\mathrm{1}.\mathrm{25}\vee{t}\approx.\mathrm{661}\pm\mathrm{1}.\mathrm{14} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{at}\:\mathrm{all} \\ $$
Answered by SEKRET last updated on 21/Jan/21

$$\mathrm{10} \\ $$
Answered by SEKRET last updated on 21/Jan/21
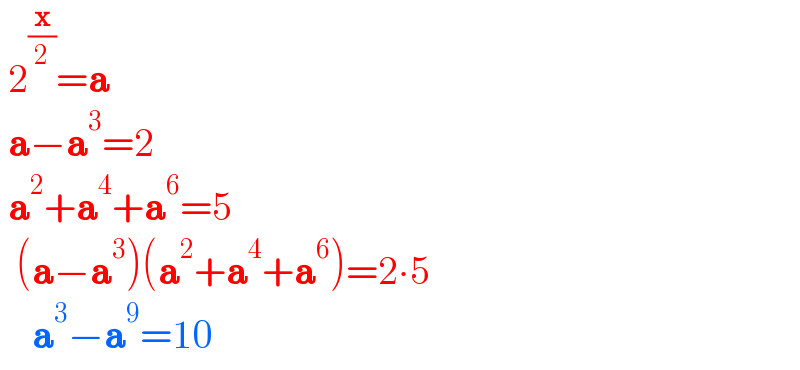
$$\:\mathrm{2}^{\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}} =\boldsymbol{\mathrm{a}} \\ $$$$\:\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{a}}^{\mathrm{3}} =\mathrm{2} \\ $$$$\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\boldsymbol{\mathrm{a}}^{\mathrm{6}} =\mathrm{5} \\ $$$$\:\:\left(\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{a}}^{\mathrm{3}} \right)\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\boldsymbol{\mathrm{a}}^{\mathrm{6}} \right)=\mathrm{2}\centerdot\mathrm{5} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{a}}^{\mathrm{3}} −\boldsymbol{\mathrm{a}}^{\mathrm{9}} =\mathrm{10} \\ $$
Commented by MJS_new last updated on 21/Jan/21
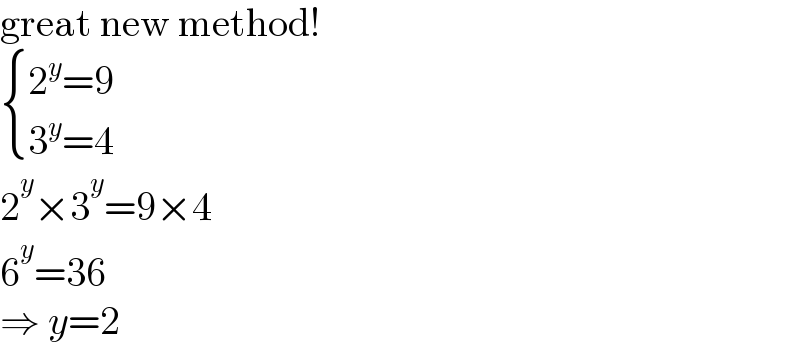
$$\mathrm{great}\:\mathrm{new}\:\mathrm{method}! \\ $$$$\begin{cases}{\mathrm{2}^{{y}} =\mathrm{9}}\\{\mathrm{3}^{{y}} =\mathrm{4}}\end{cases} \\ $$$$\mathrm{2}^{{y}} ×\mathrm{3}^{{y}} =\mathrm{9}×\mathrm{4} \\ $$$$\mathrm{6}^{{y}} =\mathrm{36} \\ $$$$\Rightarrow\:{y}=\mathrm{2} \\ $$
Answered by bemath last updated on 21/Jan/21
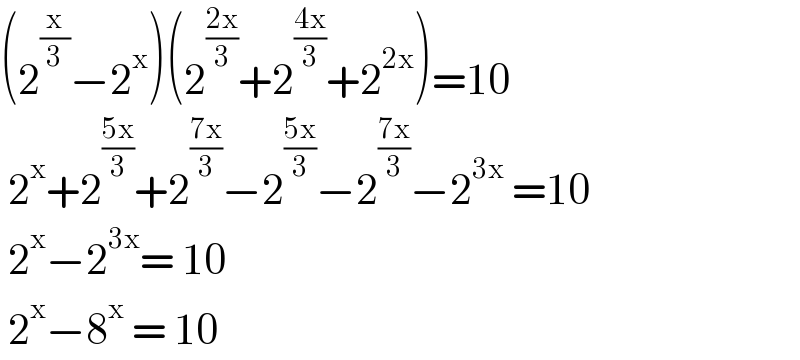
$$\left(\mathrm{2}^{\frac{\mathrm{x}}{\mathrm{3}}} −\mathrm{2}^{\mathrm{x}} \right)\left(\mathrm{2}^{\frac{\mathrm{2x}}{\mathrm{3}}} +\mathrm{2}^{\frac{\mathrm{4x}}{\mathrm{3}}} +\mathrm{2}^{\mathrm{2x}} \right)=\mathrm{10} \\ $$$$\:\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\frac{\mathrm{5x}}{\mathrm{3}}} +\mathrm{2}^{\frac{\mathrm{7x}}{\mathrm{3}}} −\mathrm{2}^{\frac{\mathrm{5x}}{\mathrm{3}}} −\mathrm{2}^{\frac{\mathrm{7x}}{\mathrm{3}}} −\mathrm{2}^{\mathrm{3x}} \:=\mathrm{10} \\ $$$$\:\mathrm{2}^{\mathrm{x}} −\mathrm{2}^{\mathrm{3x}} =\:\mathrm{10} \\ $$$$\:\mathrm{2}^{\mathrm{x}} −\mathrm{8}^{\mathrm{x}} \:=\:\mathrm{10} \\ $$
Commented by MJS_new last updated on 21/Jan/21

$$\mathrm{people},\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}!\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:{x}\:\mathrm{solving} \\ $$$$\mathrm{both}\:\mathrm{equations}\:\mathrm{as}\:\mathrm{I}\:\mathrm{showed}.\:\mathrm{multiplying} \\ $$$$\mathrm{two}\:\mathrm{equations}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\mathrm{in}\:\mathrm{case}\:\mathrm{the} \\ $$$$\mathrm{variables}\:\mathrm{are}\:\mathrm{not}\:\mathrm{the}\:\mathrm{same} \\ $$$$\begin{cases}{{x}=\mathrm{5}}\\{{x}=\mathrm{3}}\end{cases} \\ $$$$\overset{?} {\Rightarrow}\:{x}^{\mathrm{2}} =\mathrm{15} \\ $$
Commented by liberty last updated on 21/Jan/21
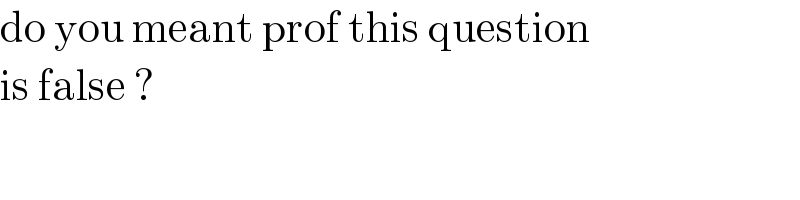
$$\mathrm{do}\:\mathrm{you}\:\mathrm{meant}\:\mathrm{prof}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{is}\:\mathrm{false}\:? \\ $$
Commented by MJS_new last updated on 21/Jan/21

$$\mathrm{obviously} \\ $$
Commented by liberty last updated on 21/Jan/21

$$\mathrm{yes}.\:\mathrm{i}\:\mathrm{agree} \\ $$
