Question Number 130188 by SEKRET last updated on 23/Jan/21

Answered by Lordose last updated on 23/Jan/21
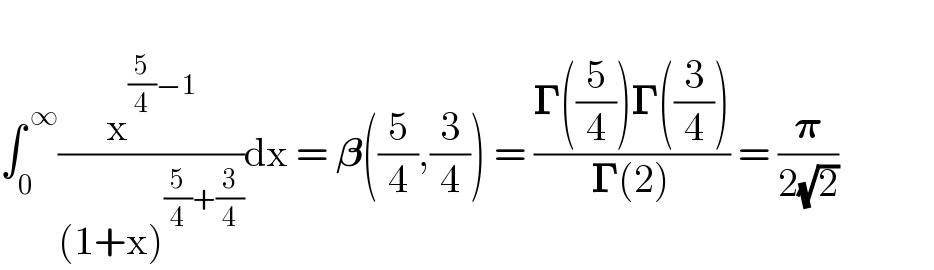
$$ \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} }\mathrm{dx}\:=\:\boldsymbol{\beta}\left(\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{3}}{\mathrm{4}}\right)\:=\:\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2}\right)}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by SEKRET last updated on 23/Jan/21

$$\boldsymbol{\mathrm{thank}}\:\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{sir}}\:\:\boldsymbol{\mathrm{eyler}}\:\boldsymbol{\mathrm{betta}}\:\:\mathrm{5}\:\:\boldsymbol{\mathrm{like}} \\ $$
