Question-130339

Question Number 130339 by mnjuly1970 last updated on 24/Jan/21

Answered by MJS_new last updated on 25/Jan/21

A= ((0),(a) ) B= ((0),(0) ) C= ((c),(0) ) AC: y=−(a/c)x+a 0≤d∈R BD: y=dx D= ((((ac)/(a+cd))),(((acd)/(a+cd))) ) radius of incircle ABD ((ac)/(a+cd+(√(a^2 +c^2 ))+c(√(d^2 +1))))=r_(ABD) radius of incircle BCD ((acd)/(a+cd+d(√(a^2 +c^2 ))+a(√(d^2 +1))))=r_(BCD) r_(ABD) =r_(BCD) leads to (a−cd)(√(d^2 +1))=(a+cd)(d−1) ⇒ d=(((a(√2)+(√(ac))−c(√2))(√a))/( (2a−c)(√c))) this means, for any rectangular triangle we can find a d in order to get 2 part triangles with equal incircles (lim_(c→2a) d =(3/4)) now we know ∣BD∣=13 ((ac(√(d^2 +1)))/(a+cd))=13 the question is if the area is unique under these conditions indeed because of a>0∧c>0 inserting for d we get ac=338 ⇒ area is ((ac)/2)=169

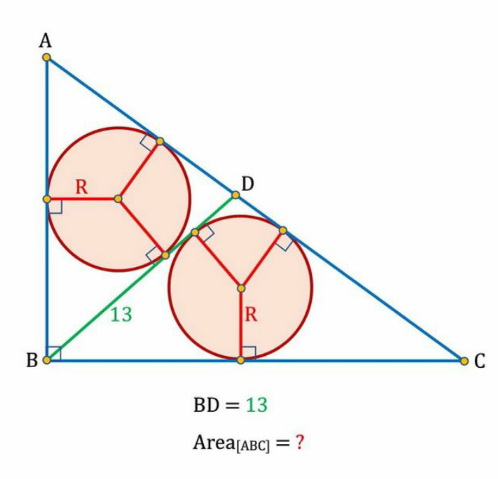
$${A}=\begin{pmatrix}{\mathrm{0}}\\{{a}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{{c}}\\{\mathrm{0}}\end{pmatrix} \\ $$$${AC}:\:{y}=−\frac{{a}}{{c}}{x}+{a} \\ $$$$\mathrm{0}\leqslant{d}\in\mathbb{R} \\ $$$${BD}:\:{y}={dx} \\ $$$${D}=\begin{pmatrix}{\frac{{ac}}{{a}+{cd}}}\\{\frac{{acd}}{{a}+{cd}}}\end{pmatrix} \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{incircle}\:{ABD} \\ $$$$\frac{{ac}}{{a}+{cd}+\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }+{c}\sqrt{{d}^{\mathrm{2}} +\mathrm{1}}}={r}_{{ABD}} \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{incircle}\:{BCD} \\ $$$$\frac{{acd}}{{a}+{cd}+{d}\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }+{a}\sqrt{{d}^{\mathrm{2}} +\mathrm{1}}}={r}_{{BCD}} \\ $$$${r}_{{ABD}} ={r}_{{BCD}} \:\mathrm{leads}\:\mathrm{to} \\ $$$$\left({a}−{cd}\right)\sqrt{{d}^{\mathrm{2}} +\mathrm{1}}=\left({a}+{cd}\right)\left({d}−\mathrm{1}\right) \\ $$$$\Rightarrow\:{d}=\frac{\left({a}\sqrt{\mathrm{2}}+\sqrt{{ac}}−{c}\sqrt{\mathrm{2}}\right)\sqrt{{a}}}{\:\left(\mathrm{2}{a}−{c}\right)\sqrt{{c}}} \\ $$$$\mathrm{this}\:\mathrm{means},\:\mathrm{for}\:\mathrm{any}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{find}\:\mathrm{a}\:{d}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{get}\:\mathrm{2}\:\mathrm{part}\:\mathrm{triangles} \\ $$$$\mathrm{with}\:\mathrm{equal}\:\mathrm{incircles}\:\left(\underset{{c}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:{d}\:=\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{know}\:\mid{BD}\mid=\mathrm{13} \\ $$$$\frac{{ac}\sqrt{{d}^{\mathrm{2}} +\mathrm{1}}}{{a}+{cd}}=\mathrm{13} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{if}\:\mathrm{the}\:\mathrm{area}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{under} \\ $$$$\mathrm{these}\:\mathrm{conditions} \\ $$$$\mathrm{indeed}\:\mathrm{because}\:\mathrm{of}\:{a}>\mathrm{0}\wedge{c}>\mathrm{0}\:\mathrm{inserting}\:\mathrm{for}\:{d} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$${ac}=\mathrm{338} \\ $$$$\Rightarrow\:\mathrm{area}\:\mathrm{is}\:\frac{{ac}}{\mathrm{2}}=\mathrm{169} \\ $$

Commented by mnjuly1970 last updated on 25/Jan/21

$${grateful}\:\:{mr}\:{mjs}.{thanks}\:{alot}… \\ $$

Answered by Olaf last updated on 24/Jan/21

By symmetry AB = BC D middle of [AC] BD = AD = DC AC = 26 Area[ABC] = (1/2)AC×BD = 169

$$\mathrm{By}\:\mathrm{symmetry}\:\mathrm{AB}\:=\:\mathrm{BC} \\ $$$$\mathrm{D}\:\mathrm{middle}\:\mathrm{of}\:\left[\mathrm{AC}\right] \\ $$$$\mathrm{BD}\:=\:\mathrm{AD}\:=\:\mathrm{DC} \\ $$$$\mathrm{AC}\:=\:\mathrm{26} \\ $$$$\mathrm{Area}\left[\mathrm{ABC}\right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AC}×\mathrm{BD}\:=\:\mathrm{169} \\ $$

Commented by MJS_new last updated on 25/Jan/21

it′s not necessary to have ∣AB∣=∣BC∣. it′s always true for ∣AB∣×∣BC∣=338

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{necessary}\:\mathrm{to}\:\mathrm{have}\:\mid{AB}\mid=\mid{BC}\mid.\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{always}\:\mathrm{true}\:\mathrm{for}\:\mid{AB}\mid×\mid{BC}\mid=\mathrm{338} \\ $$

Commented by mnjuly1970 last updated on 25/Jan/21

$${perfect}.{thank}\:{you}\:{mr}\:{olaf}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply