Question Number 130370 by gowsalya last updated on 24/Jan/21
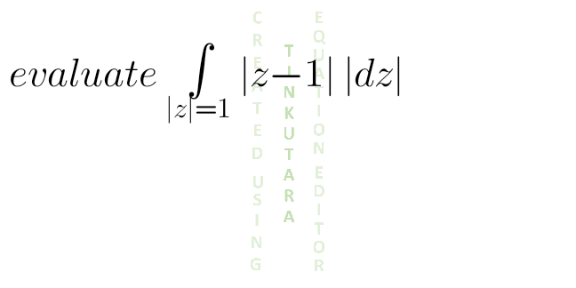
Answered by TheSupreme last updated on 24/Jan/21
![z=e^(iθ) ∣dz∣=∣ie^(iθ) dθ∣=dθ ∫_0 ^(2π) ∣e^(iθ) −1∣dθ ∫_0 ^(2π) (√((cos(θ)−1)^2 +sin^2 θ))dθ ∫_0 ^(2π) (√(2−2cos(θ)))dθ • cos(2γ)=1−2sin^2 (γ) 2sin^2 (γ)=1−cos(2γ) ∫_0 ^(2π) 2sin((θ/2))dθ=[−4cos((θ/2))]_0 ^(2π) =8](https://www.tinkutara.com/question/Q130373.png)
$${z}={e}^{{i}\theta} \\ $$$$\mid{dz}\mid=\mid{ie}^{{i}\theta} {d}\theta\mid={d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid{e}^{{i}\theta} −\mathrm{1}\mid{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{\left({cos}\left(\theta\right)−\mathrm{1}\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \theta}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{\mathrm{2}−\mathrm{2}{cos}\left(\theta\right)}{d}\theta \\ $$$$\bullet\:{cos}\left(\mathrm{2}\gamma\right)=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\gamma\right) \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} \left(\gamma\right)=\mathrm{1}−{cos}\left(\mathrm{2}\gamma\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{2}{sin}\left(\frac{\theta}{\mathrm{2}}\right){d}\theta=\left[−\mathrm{4}{cos}\left(\frac{\theta}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\mathrm{8} \\ $$$$ \\ $$
Commented by gowsalya last updated on 25/Jan/21
Thank u
Answered by Olaf last updated on 24/Jan/21
![Ω = ∫_(∣z∣=1) ∣z−1∣∣dz∣ Ω = ∫_0 ^(2π) ∣e^(iθ) −1∣∣ie^(iθ) dθ∣ Ω = ∫_0 ^(2π) ∣2ie^(i(θ/2)) ∣∣((e^(i(θ/2)) −e^(−i(θ/2)) )/(2i))∣dθ Ω = 2∫_0 ^(2π) ∣sin(θ/2)∣dθ Ω = 2∫_0 ^(2π) sin(θ/2)dθ Ω = 4[−cos(θ/2)]_0 ^(2π) Ω = 8](https://www.tinkutara.com/question/Q130374.png)
$$\Omega\:=\:\int_{\mid{z}\mid=\mathrm{1}} \mid{z}−\mathrm{1}\mid\mid{dz}\mid \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid{e}^{{i}\theta} −\mathrm{1}\mid\mid{ie}^{{i}\theta} {d}\theta\mid \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid\mathrm{2}{ie}^{{i}\frac{\theta}{\mathrm{2}}} \mid\mid\frac{{e}^{{i}\frac{\theta}{\mathrm{2}}} −{e}^{−{i}\frac{\theta}{\mathrm{2}}} }{\mathrm{2}{i}}\mid{d}\theta \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid\mathrm{sin}\frac{\theta}{\mathrm{2}}\mid{d}\theta \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{sin}\frac{\theta}{\mathrm{2}}{d}\theta \\ $$$$\Omega\:=\:\mathrm{4}\left[−\mathrm{cos}\frac{\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\Omega\:=\:\mathrm{8} \\ $$
Commented by gowsalya last updated on 25/Jan/21
Thank u
