Question Number 130440 by mohammad17 last updated on 25/Jan/21
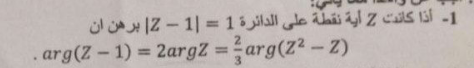
Commented by mohammad17 last updated on 25/Jan/21

$${help}\:{me} \\ $$
Answered by mathmax by abdo last updated on 25/Jan/21
![∣z−1∣=1 ⇒z−1=e^(iθ) with θ ∈]0,2π[ ⇒z=1+e^(iθ) z=1+cosθ+ isinθ =2cos^2 ((θ/2))+2isin((θ/2))cos((θ/2)) =2cos((θ/2))e^((iθ)/2) if cos((θ/2))>0 ⇒argz=(θ/2) ⇒2argz=θ arg(z−1) (2/3)arg(z^2 −z)=(2/3)arg(z(z−1))=(2/3){argz +arg(z−1)} =(2/3){(θ/2) +θ} =(2/3)×(3/2)θ =θ=arg(z−1) we use the same proof if cos((θ/2))<0 because z=−2cos((θ/2))e^(iπ) .e^((iθ)/2) =−2cos((θ/2))e^(i(π+(θ/2))) ⇒argz=π+(θ/2) the equality is modulo 2π.](https://www.tinkutara.com/question/Q130457.png)
$$\left.\mid\mathrm{z}−\mathrm{1}\mid=\mathrm{1}\:\Rightarrow\mathrm{z}−\mathrm{1}=\mathrm{e}^{\mathrm{i}\theta} \:\:\:\:\:\:\mathrm{with}\:\theta\:\in\right]\mathrm{0},\mathrm{2}\pi\left[\:\Rightarrow\mathrm{z}=\mathrm{1}+\mathrm{e}^{\mathrm{i}\theta} \right. \\ $$$$\mathrm{z}=\mathrm{1}+\mathrm{cos}\theta+\:\mathrm{isin}\theta\:=\mathrm{2cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{2isin}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2cos}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{2}}} \:\:\mathrm{if}\:\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow\mathrm{argz}=\frac{\theta}{\mathrm{2}}\:\Rightarrow\mathrm{2argz}=\theta\:\mathrm{arg}\left(\mathrm{z}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arg}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}\right)=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arg}\left(\mathrm{z}\left(\mathrm{z}−\mathrm{1}\right)\right)=\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{argz}\:+\mathrm{arg}\left(\mathrm{z}−\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left\{\frac{\theta}{\mathrm{2}}\:+\theta\right\}\:=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{2}}\theta\:=\theta=\mathrm{arg}\left(\mathrm{z}−\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{same}\:\mathrm{proof}\:\mathrm{if}\:\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)<\mathrm{0}\:\mathrm{because} \\ $$$$\mathrm{z}=−\mathrm{2cos}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{e}^{\mathrm{i}\pi} .\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{2}}} \:=−\mathrm{2cos}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{e}^{\mathrm{i}\left(\pi+\frac{\theta}{\mathrm{2}}\right)} \:\Rightarrow\mathrm{argz}=\pi+\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{equality}\:\mathrm{is}\:\mathrm{modulo}\:\mathrm{2}\pi. \\ $$
