Question Number 130537 by benjo_mathlover last updated on 26/Jan/21

Answered by EDWIN88 last updated on 26/Jan/21
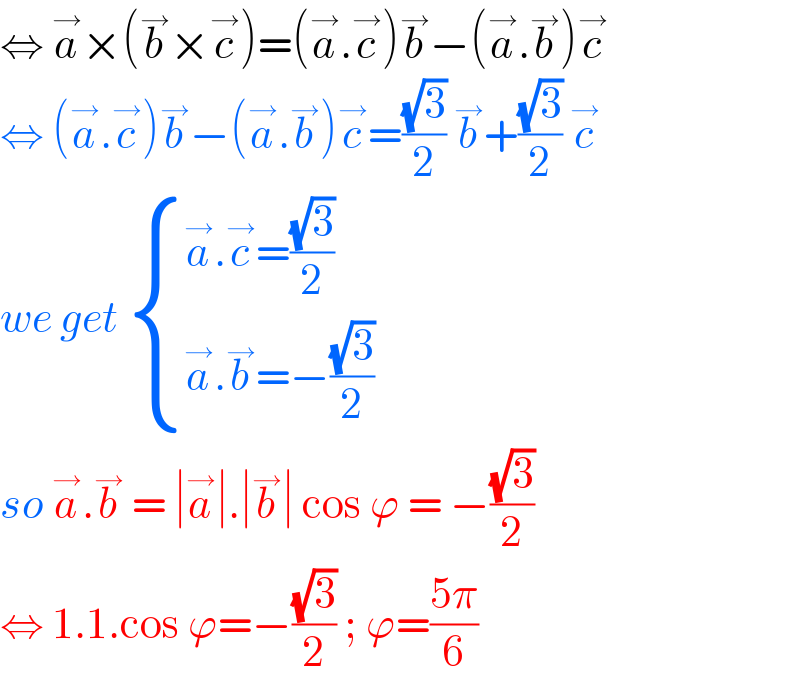
$$\Leftrightarrow\:\overset{\rightarrow} {{a}}×\left(\overset{\rightarrow} {{b}}×\overset{\rightarrow} {{c}}\right)=\left(\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}\right)\overset{\rightarrow} {{b}}−\left(\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}\right)\overset{\rightarrow} {{c}} \\ $$$$\Leftrightarrow\:\left(\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}\right)\overset{\rightarrow} {{b}}−\left(\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}\right)\overset{\rightarrow} {{c}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\overset{\rightarrow} {{b}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\overset{\rightarrow} {{c}} \\ $$$${we}\:{get}\:\begin{cases}{\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{cases} \\ $$$${so}\:\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}\:=\:\mid\overset{\rightarrow} {{a}}\mid.\mid\overset{\rightarrow} {{b}}\mid\:\mathrm{cos}\:\varphi\:=\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{1}.\mathrm{1}.\mathrm{cos}\:\varphi=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:;\:\varphi=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$
