Question Number 130649 by muneer0o0 last updated on 27/Jan/21
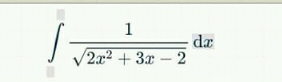
Answered by MJS_new last updated on 27/Jan/21
![∫(dx/( (√(2x^2 +3x−2))))=((√2)/2)∫(dx/( (√(x^2 +(3/2)x−1))))= [t=x+(3/4) → dx=dt] =((√2)/2)∫(dt/( (√(t^2 −((25)/(16))))))= [u=(4/5)(t+(√(t^2 −((25)/(16))))) → dt=((5(√(t^2 −((25)/(16)))))/(4(t+(√(t^2 −((25)/(16))))))du] =((√2)/2)∫(du/u)=((√2)/2)ln u =... =((√2)/2)ln (4x+3+2(√(2(2x^2 +3x−2)))) +C](https://www.tinkutara.com/question/Q130650.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{x}−\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\frac{\mathrm{3}}{\mathrm{4}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{16}}}}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\mathrm{4}}{\mathrm{5}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{16}}}\right)\:\rightarrow\:{dt}=\frac{\mathrm{5}\sqrt{{t}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{16}}}}{\mathrm{4}\left({t}+\sqrt{{t}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{16}}}\right.}{du}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{du}}{{u}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:{u}\:=… \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{4}{x}+\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\right)}\right)\:+{C} \\ $$
Answered by mathmax by abdo last updated on 27/Jan/21

$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}} \\ $$$$\Delta=\mathrm{9}−\mathrm{4}\left(−\mathrm{4}\right)=\mathrm{25}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{3}+\mathrm{5}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{3}−\mathrm{5}}{\mathrm{4}}=−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}=\mathrm{2}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{x}+\mathrm{2}\right)\:=\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\left.\:\sqrt{\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right.}\right)}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{x}+\mathrm{2}}=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{2tdt}}{\mathrm{t}\sqrt{\mathrm{2t}^{\mathrm{2}} −\mathrm{4}−\mathrm{1}}}\:=\mathrm{2}\int\:\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2t}^{\mathrm{2}} −\mathrm{5}}}\:=\sqrt{\mathrm{2}}\int\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}}} \\ $$$$=_{\mathrm{t}=\sqrt{\frac{\mathrm{5}}{\mathrm{2}}}\mathrm{y}} \:\:\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{5}}{\mathrm{2}}}\sqrt{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}}.\sqrt{\frac{\mathrm{5}}{\mathrm{2}}}\mathrm{dy}\:=\sqrt{\mathrm{2}}\int\:\frac{\mathrm{dy}}{\:\sqrt{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{y}+\sqrt{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}\right)\:+\mathrm{c} \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{5}}}\mathrm{t}+\sqrt{\frac{\mathrm{2}}{\mathrm{5}}\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{c} \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{5}}}\sqrt{\mathrm{x}+\mathrm{2}}\:+\sqrt{\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{x}+\mathrm{2}\right)−\mathrm{1}}\right)\:+\mathrm{c} \\ $$
Answered by PNL last updated on 29/Jan/21

$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\:=\mathrm{0} \\ $$
