Question-130701

Question Number 130701 by mohammad17 last updated on 28/Jan/21

Answered by mathmax by abdo last updated on 28/Jan/21

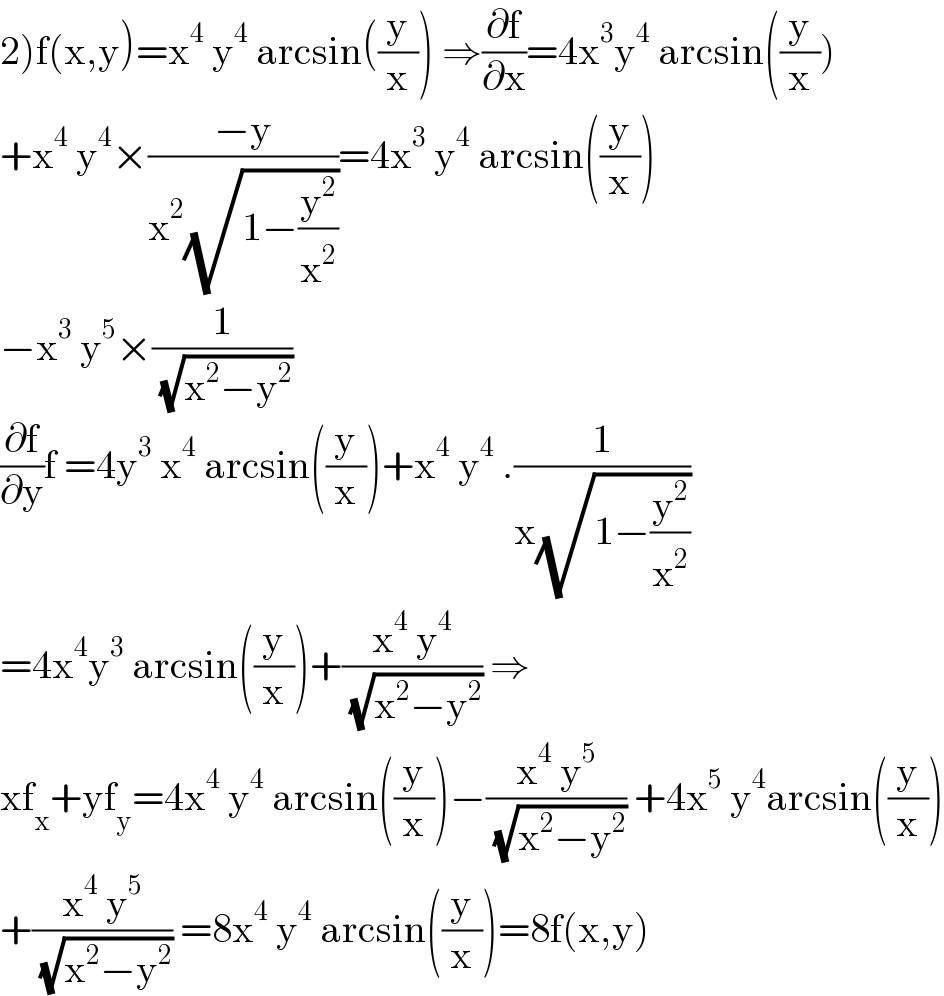
2)f(x,y)=x^4 y^4 arcsin((y/x)) ⇒(∂f/∂x)=4x^3 y^4 arcsin((y/x)) +x^4 y^4 ×((−y)/(x^2 (√(1−(y^2 /x^2 )))))=4x^3 y^4 arcsin((y/x)) −x^3 y^5 ×(1/( (√(x^2 −y^2 )))) (∂f/∂y)f =4y^3 x^4 arcsin((y/x))+x^4 y^4 .(1/(x(√(1−(y^2 /x^2 ))))) =4x^4 y^3 arcsin((y/x))+((x^4 y^4 )/( (√(x^2 −y^2 )))) ⇒ xf_x +yf_y =4x^4 y^4 arcsin((y/x))−((x^4 y^5 )/( (√(x^2 −y^2 )))) +4x^5 y^4 arcsin((y/x)) +((x^4 y^5 )/( (√(x^2 −y^2 )))) =8x^4 y^4 arcsin((y/x))=8f(x,y)

$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\:\Rightarrow\frac{\partial\mathrm{f}}{\partial\mathrm{x}}=\mathrm{4x}^{\mathrm{3}} \mathrm{y}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$+\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} ×\frac{−\mathrm{y}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}}=\mathrm{4x}^{\mathrm{3}} \:\mathrm{y}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$−\mathrm{x}^{\mathrm{3}} \:\mathrm{y}^{\mathrm{5}} ×\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }} \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\mathrm{f}\:=\mathrm{4y}^{\mathrm{3}} \:\mathrm{x}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)+\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} \:.\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{1}−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}} \\ $$$$=\mathrm{4x}^{\mathrm{4}} \mathrm{y}^{\mathrm{3}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)+\frac{\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\mathrm{xf}_{\mathrm{x}} +\mathrm{yf}_{\mathrm{y}} =\mathrm{4x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\frac{\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{5}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}\:+\mathrm{4x}^{\mathrm{5}} \:\mathrm{y}^{\mathrm{4}} \mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$+\frac{\mathrm{x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{5}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}\:=\mathrm{8x}^{\mathrm{4}} \:\mathrm{y}^{\mathrm{4}} \:\mathrm{arcsin}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)=\mathrm{8f}\left(\mathrm{x},\mathrm{y}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply