Question Number 130780 by LYKA last updated on 28/Jan/21

Commented by kaivan.ahmadi last updated on 29/Jan/21
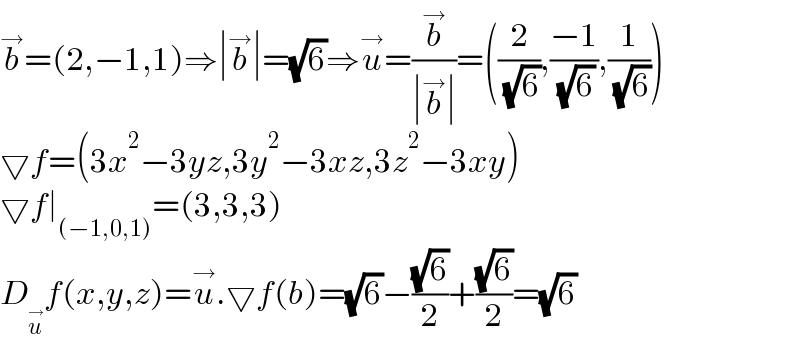
$$\overset{\rightarrow} {{b}}=\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right)\Rightarrow\mid\overset{\rightarrow} {{b}}\mid=\sqrt{\mathrm{6}}\Rightarrow\overset{\rightarrow} {{u}}=\frac{\overset{\rightarrow} {{b}}}{\mid\overset{\rightarrow} {{b}}\mid}=\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}},\frac{−\mathrm{1}}{\:\sqrt{\mathrm{6}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\right) \\ $$$$\bigtriangledown{f}=\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{yz},\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{xz},\mathrm{3}{z}^{\mathrm{2}} −\mathrm{3}{xy}\right) \\ $$$$\bigtriangledown{f}\mid_{\left(−\mathrm{1},\mathrm{0},\mathrm{1}\right)} =\left(\mathrm{3},\mathrm{3},\mathrm{3}\right) \\ $$$${D}_{\overset{\rightarrow} {{u}}} {f}\left({x},{y},{z}\right)=\overset{\rightarrow} {{u}}.\bigtriangledown{f}\left({b}\right)=\sqrt{\mathrm{6}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}=\sqrt{\mathrm{6}} \\ $$
