Question-130802

Question Number 130802 by shaker last updated on 29/Jan/21

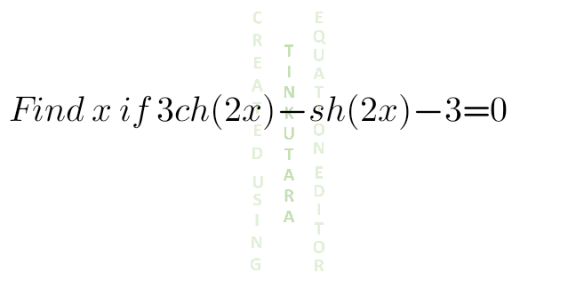
Answered by TheSupreme last updated on 29/Jan/21

Assuming ch=cosh 3cosh(2x)−sinh(2x)−3=0 3(((e^(2x) +e^(−2x) )/2))−((e^(2x) −e^(−2x) )/2)=3 e^(2x) +2e^(−2x) −3=0 e^(4x) −3e^(2x) +2=0 e^(2x) =t t^2 −3t+2=0 (t−1)(t−2)=0 e^(2x) =1→x=0 e^(2x) =2→x=(1/2)ln(2)

$${Assuming}\:{ch}={cosh} \\ $$$$\mathrm{3}{cosh}\left(\mathrm{2}{x}\right)−{sinh}\left(\mathrm{2}{x}\right)−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}\left(\frac{{e}^{\mathrm{2}{x}} +{e}^{−\mathrm{2}{x}} }{\mathrm{2}}\right)−\frac{{e}^{\mathrm{2}{x}} −{e}^{−\mathrm{2}{x}} }{\mathrm{2}}=\mathrm{3} \\ $$$${e}^{\mathrm{2}{x}} +\mathrm{2}{e}^{−\mathrm{2}{x}} −\mathrm{3}=\mathrm{0} \\ $$$${e}^{\mathrm{4}{x}} −\mathrm{3}{e}^{\mathrm{2}{x}} +\mathrm{2}=\mathrm{0} \\ $$$${e}^{\mathrm{2}{x}} ={t} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{2}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}−\mathrm{2}\right)=\mathrm{0} \\ $$$${e}^{\mathrm{2}{x}} =\mathrm{1}\rightarrow{x}=\mathrm{0} \\ $$$${e}^{\mathrm{2}{x}} =\mathrm{2}\rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Answered by Olaf last updated on 29/Jan/21

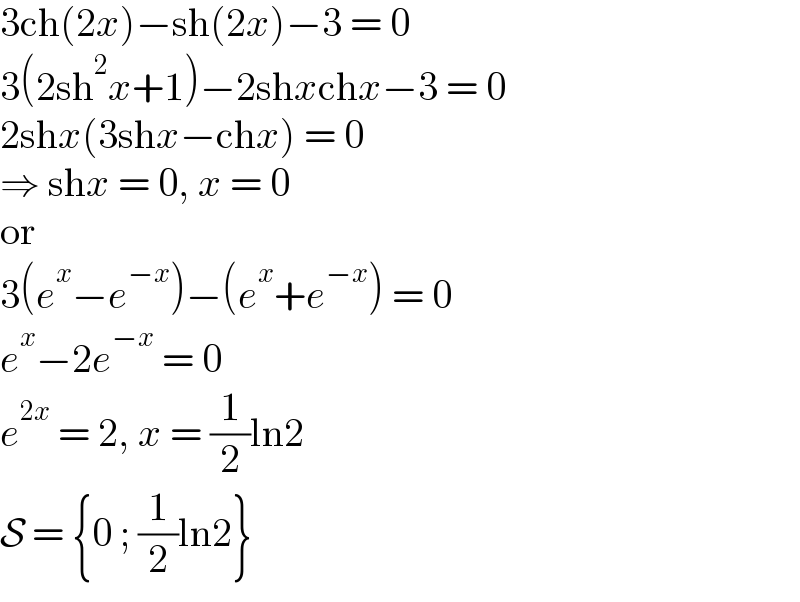
3ch(2x)−sh(2x)−3 = 0 3(2sh^2 x+1)−2shxchx−3 = 0 2shx(3shx−chx) = 0 ⇒ shx = 0, x = 0 or 3(e^x −e^(−x) )−(e^x +e^(−x) ) = 0 e^x −2e^(−x) = 0 e^(2x) = 2, x = (1/2)ln2 S = {0 ; (1/2)ln2}

$$\mathrm{3ch}\left(\mathrm{2}{x}\right)−\mathrm{sh}\left(\mathrm{2}{x}\right)−\mathrm{3}\:=\:\mathrm{0} \\ $$$$\mathrm{3}\left(\mathrm{2sh}^{\mathrm{2}} {x}+\mathrm{1}\right)−\mathrm{2sh}{x}\mathrm{ch}{x}−\mathrm{3}\:=\:\mathrm{0} \\ $$$$\mathrm{2sh}{x}\left(\mathrm{3sh}{x}−\mathrm{ch}{x}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{sh}{x}\:=\:\mathrm{0},\:{x}\:=\:\mathrm{0} \\ $$$$\mathrm{or} \\ $$$$\mathrm{3}\left({e}^{{x}} −{e}^{−{x}} \right)−\left({e}^{{x}} +{e}^{−{x}} \right)\:=\:\mathrm{0} \\ $$$${e}^{{x}} −\mathrm{2}{e}^{−{x}} \:=\:\mathrm{0} \\ $$$${e}^{\mathrm{2}{x}} \:=\:\mathrm{2},\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2} \\ $$$$\mathcal{S}\:=\:\left\{\mathrm{0}\:;\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}\right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply