Question Number 130806 by shaker last updated on 29/Jan/21
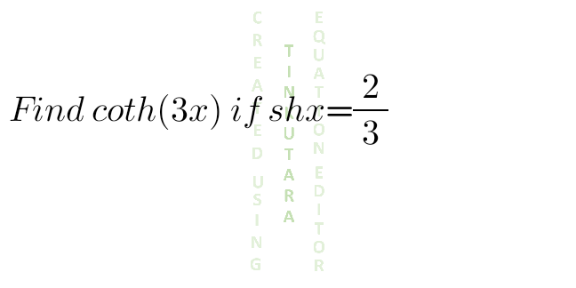
Answered by Olaf last updated on 29/Jan/21
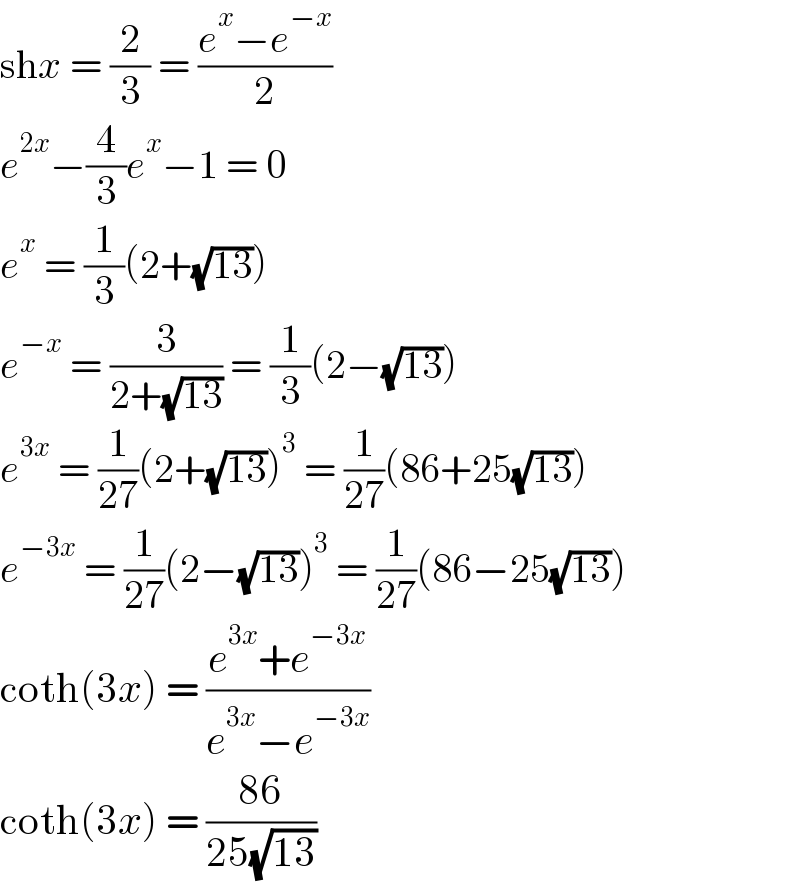
$$\mathrm{sh}{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:=\:\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$${e}^{\mathrm{2}{x}} −\frac{\mathrm{4}}{\mathrm{3}}{e}^{{x}} −\mathrm{1}\:=\:\mathrm{0} \\ $$$${e}^{{x}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}+\sqrt{\mathrm{13}}\right) \\ $$$${e}^{−{x}} \:=\:\frac{\mathrm{3}}{\mathrm{2}+\sqrt{\mathrm{13}}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}−\sqrt{\mathrm{13}}\right) \\ $$$${e}^{\mathrm{3}{x}} \:=\:\frac{\mathrm{1}}{\mathrm{27}}\left(\mathrm{2}+\sqrt{\mathrm{13}}\right)^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{27}}\left(\mathrm{86}+\mathrm{25}\sqrt{\mathrm{13}}\right) \\ $$$${e}^{−\mathrm{3}{x}} \:=\:\frac{\mathrm{1}}{\mathrm{27}}\left(\mathrm{2}−\sqrt{\mathrm{13}}\right)^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{27}}\left(\mathrm{86}−\mathrm{25}\sqrt{\mathrm{13}}\right) \\ $$$$\mathrm{coth}\left(\mathrm{3}{x}\right)\:=\:\frac{{e}^{\mathrm{3}{x}} +{e}^{−\mathrm{3}{x}} }{{e}^{\mathrm{3}{x}} −{e}^{−\mathrm{3}{x}} } \\ $$$$\mathrm{coth}\left(\mathrm{3}{x}\right)\:=\:\frac{\mathrm{86}}{\mathrm{25}\sqrt{\mathrm{13}}} \\ $$
