Question Number 130817 by shaker last updated on 29/Jan/21
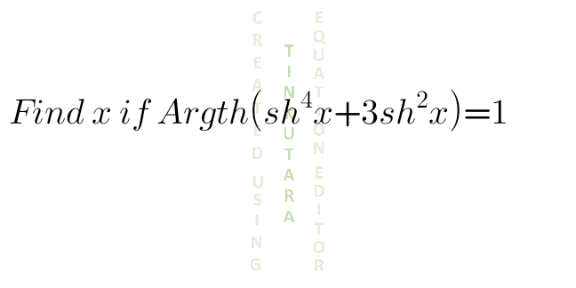
Answered by Olaf last updated on 29/Jan/21

$$\mathrm{argth}\left(\mathrm{sh}^{\mathrm{4}} {x}+\mathrm{3sh}^{\mathrm{2}} {x}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{sh}^{\mathrm{4}} {x}+\mathrm{3sh}^{\mathrm{2}} {x}\:=\:\mathrm{th}\left(\mathrm{1}\right)\:=\:\frac{{e}−\frac{\mathrm{1}}{{e}}}{{e}+\frac{\mathrm{1}}{{e}}}\:=\:\frac{{e}^{\mathrm{2}} −\mathrm{1}}{{e}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{sh}^{\mathrm{4}} {x}+\mathrm{3sh}^{\mathrm{2}} {x}−\frac{{e}^{\mathrm{2}} −\mathrm{1}}{{e}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{0} \\ $$$$\mathrm{sh}^{\mathrm{2}} {x}\:=\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}+\mathrm{4}\frac{{e}^{\mathrm{2}} −\mathrm{1}}{{e}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{2}} \\ $$$$\mathrm{sh}^{\mathrm{2}} {x}\:=\:\frac{−\mathrm{3}\pm\sqrt{\frac{\mathrm{13}{e}^{\mathrm{2}} +\mathrm{5}}{{e}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{2}} \\ $$$$\mathrm{sh}^{\mathrm{2}} {x}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{13}{e}^{\mathrm{2}} +\mathrm{5}}{{e}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\frac{\mathrm{ch}\left(\mathrm{2}{x}\right)−\mathrm{1}}{\mathrm{2}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{13}{e}^{\mathrm{2}} +\mathrm{5}}{{e}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{ch}\left(\mathrm{2}{x}\right)\:=\:−\mathrm{2}\pm\sqrt{\frac{\mathrm{13}{e}^{\mathrm{2}} +\mathrm{5}}{{e}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{argch}\left(−\mathrm{2}\pm\sqrt{\frac{\mathrm{13}{e}^{\mathrm{2}} +\mathrm{5}}{{e}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$
