Menu Close

Question-130849

Tinku Tara 0 Comments
Pin




Question Number 130849 by TITA last updated on 29/Jan/21
Commented by Ñï= last updated on 29/Jan/21
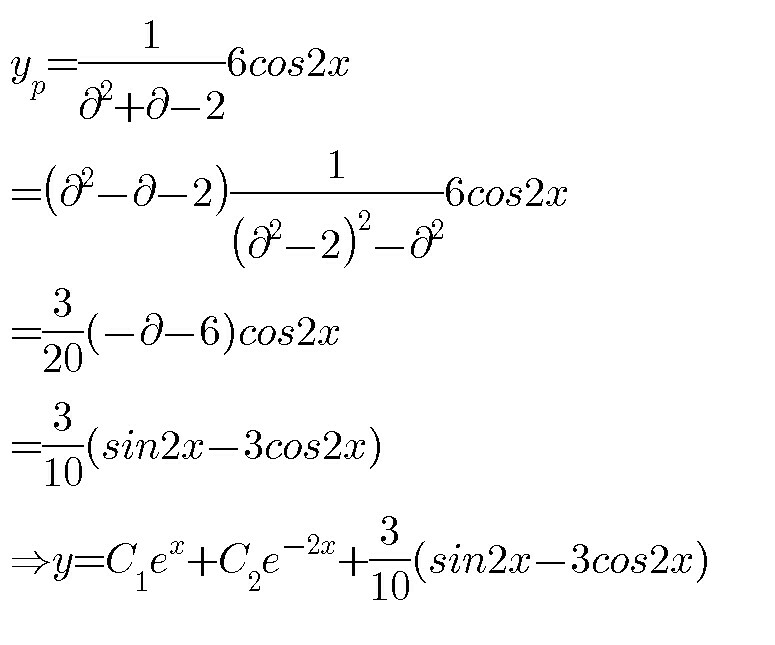
Answered by EDWIN88 last updated on 30/Jan/21
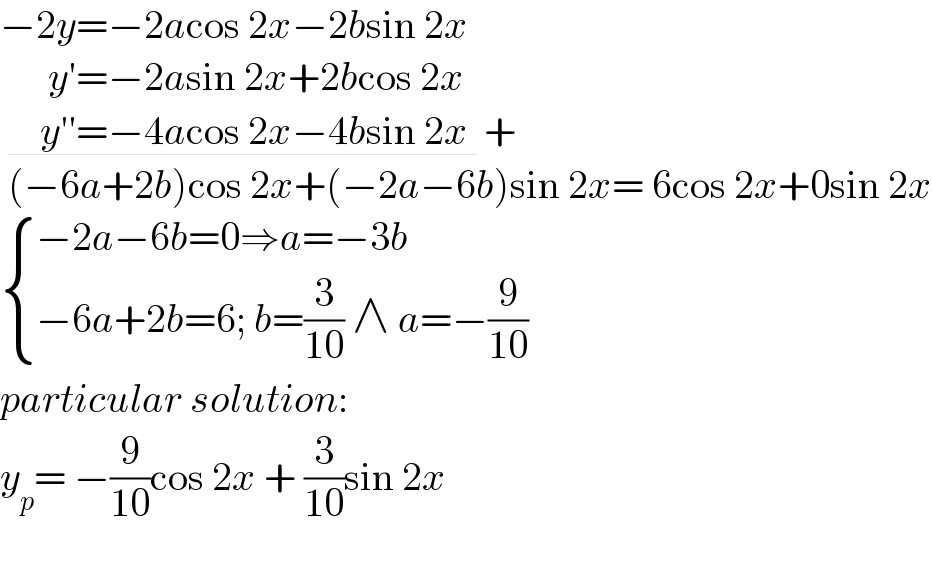
−2y=−2acos 2x−2bsin 2x y′=−2asin 2x+2bcos 2x y′′=−4acos 2x−4bsin 2x + (−6a+2b)cos 2x+(−2a−6b)sin 2x= 6cos 2x+0sin 2x { ((−2a−6b=0⇒a=−3b)),((−6a+2b=6; b=(3/(10)) ∧ a=−(9/(10)))) :} particular solution: y_p = −(9/(10))cos 2x + (3/(10))sin 2x
$$−\mathrm{2}{y}=−\mathrm{2}{a}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{2}{b}\mathrm{sin}\:\mathrm{2}{x} \\ $$$$\:\:\:\:\:\:{y}'=−\mathrm{2}{a}\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2}{b}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\:\underline{\:\:\:\:{y}''=−\mathrm{4}{a}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{4}{b}\mathrm{sin}\:\mathrm{2}{x}\:}\:+ \\ $$$$\:\left(−\mathrm{6}{a}+\mathrm{2}{b}\right)\mathrm{cos}\:\mathrm{2}{x}+\left(−\mathrm{2}{a}−\mathrm{6}{b}\right)\mathrm{sin}\:\mathrm{2}{x}=\:\mathrm{6cos}\:\mathrm{2}{x}+\mathrm{0sin}\:\mathrm{2}{x} \\ $$$$\begin{cases}{−\mathrm{2}{a}−\mathrm{6}{b}=\mathrm{0}\Rightarrow{a}=−\mathrm{3}{b}}\\{−\mathrm{6}{a}+\mathrm{2}{b}=\mathrm{6};\:{b}=\frac{\mathrm{3}}{\mathrm{10}}\:\wedge\:{a}=−\frac{\mathrm{9}}{\mathrm{10}}}\end{cases} \\ $$$${particular}\:{solution}: \\ $$$${y}_{{p}} =\:−\frac{\mathrm{9}}{\mathrm{10}}\mathrm{cos}\:\mathrm{2}{x}\:+\:\frac{\mathrm{3}}{\mathrm{10}}\mathrm{sin}\:\mathrm{2}{x}\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 30/Jan/21
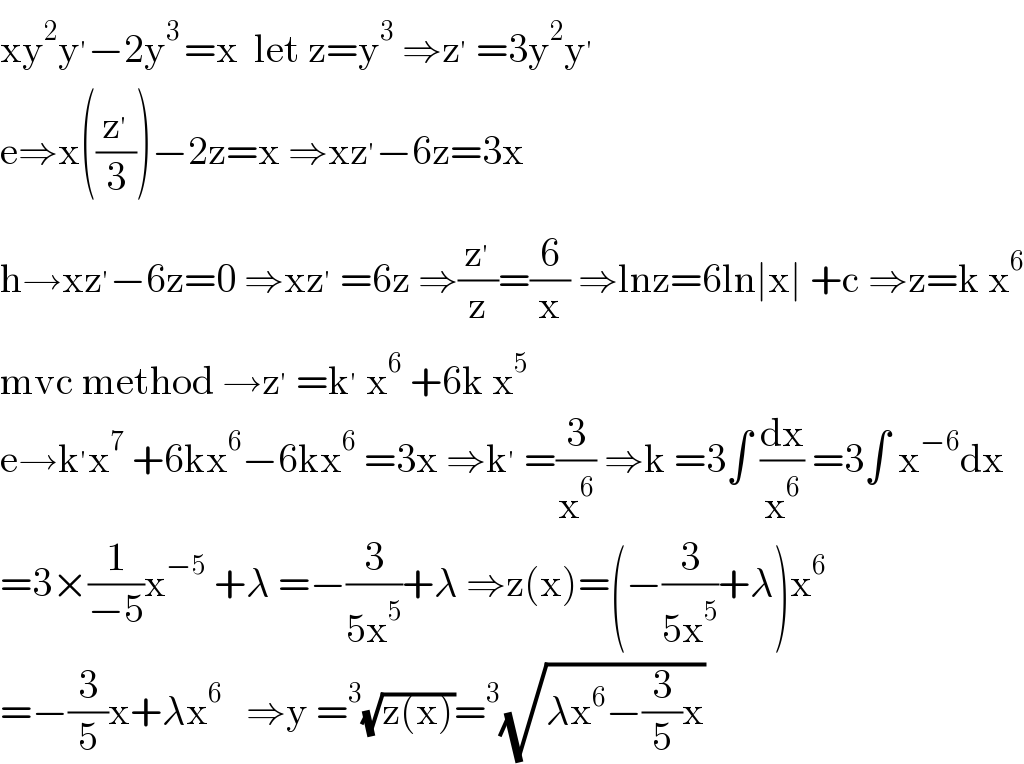
xy^2 y^′ −2y^(3 ) =x let z=y^3 ⇒z^′ =3y^2 y^′ e⇒x((z^′ /3))−2z=x ⇒xz^′ −6z=3x h→xz^′ −6z=0 ⇒xz^′ =6z ⇒(z^′ /z)=(6/x) ⇒lnz=6ln∣x∣ +c ⇒z=k x^6 mvc method →z^′ =k^′ x^6 +6k x^5 e→k^′ x^7 +6kx^6 −6kx^6 =3x ⇒k^′ =(3/x^6 ) ⇒k =3∫ (dx/x^6 ) =3∫ x^(−6) dx =3×(1/(−5))x^(−5) +λ =−(3/(5x^5 ))+λ ⇒z(x)=(−(3/(5x^5 ))+λ)x^6 =−(3/5)x+λx^6 ⇒y =^3 (√(z(x)))=^3 (√(λx^6 −(3/5)x))
$$\mathrm{xy}^{\mathrm{2}} \mathrm{y}^{'} −\mathrm{2y}^{\mathrm{3}\:} =\mathrm{x}\:\:\mathrm{let}\:\mathrm{z}=\mathrm{y}^{\mathrm{3}} \:\Rightarrow\mathrm{z}^{'} \:=\mathrm{3y}^{\mathrm{2}} \mathrm{y}^{'} \\ $$$$\mathrm{e}\Rightarrow\mathrm{x}\left(\frac{\mathrm{z}^{'} }{\mathrm{3}}\right)−\mathrm{2z}=\mathrm{x}\:\Rightarrow\mathrm{xz}^{'} −\mathrm{6z}=\mathrm{3x} \\ $$$$\mathrm{h}\rightarrow\mathrm{xz}^{'} −\mathrm{6z}=\mathrm{0}\:\Rightarrow\mathrm{xz}^{'} \:=\mathrm{6z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}=\frac{\mathrm{6}}{\mathrm{x}}\:\Rightarrow\mathrm{lnz}=\mathrm{6ln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow\mathrm{z}=\mathrm{k}\:\mathrm{x}^{\mathrm{6}} \\ $$$$\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{6}} \:+\mathrm{6k}\:\mathrm{x}^{\mathrm{5}} \\ $$$$\mathrm{e}\rightarrow\mathrm{k}^{'} \mathrm{x}^{\mathrm{7}} \:+\mathrm{6kx}^{\mathrm{6}} −\mathrm{6kx}^{\mathrm{6}} \:=\mathrm{3x}\:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{6}} }\:\Rightarrow\mathrm{k}\:=\mathrm{3}\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{6}} }\:=\mathrm{3}\int\:\mathrm{x}^{−\mathrm{6}} \mathrm{dx} \\ $$$$=\mathrm{3}×\frac{\mathrm{1}}{−\mathrm{5}}\mathrm{x}^{−\mathrm{5}} \:+\lambda\:=−\frac{\mathrm{3}}{\mathrm{5x}^{\mathrm{5}} }+\lambda\:\Rightarrow\mathrm{z}\left(\mathrm{x}\right)=\left(−\frac{\mathrm{3}}{\mathrm{5x}^{\mathrm{5}} }+\lambda\right)\mathrm{x}^{\mathrm{6}} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}+\lambda\mathrm{x}^{\mathrm{6}} \:\:\:\Rightarrow\mathrm{y}\:=^{\mathrm{3}} \sqrt{\mathrm{z}\left(\mathrm{x}\right)}=^{\mathrm{3}} \sqrt{\lambda\mathrm{x}^{\mathrm{6}} −\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}} \\ $$
Answered by mathmax by abdo last updated on 30/Jan/21
2) y^(′′) +y−2=6cos(2x) h→r^2 +r−2=0 →Δ=9 ⇒r_1 =((−1+3)/2)=1 and r_2 =((−1−3)/2)=−2 ⇒ y_h =ae^x +be^(−2x) =au_1 +bu_2 W(u_1 ,u_2 )= determinant (((e^x e^(−2x) )),((e^x −2e^(−2x) )))=−2e^(−x) −e^(−x) =−3e^(−x) ≠0 W_1 = determinant (((o e^(−2x) )),((6cos(2x) −2e^(−2x) )))=−6e^(−2x) cos(2x) W_2 = determinant (((e^(−2x) 0)),((−2e^(−x) 6cos(2x))))=6e^(−2x) cos(2x) V_1 =∫ (W_1 /W)dx =−6∫ ((e^(−2x) cos(2x))/(−3e^(−x) ))dx =2∫ e^(−x) cos(2x)dx =2 Re(∫ e^(−x+2ix) dx) and ∫ e^((−1+2i)x) dx =(1/(−1+2i))e^((−1+2i)x) =−(1/(1−2i))e^(−x) (cos(2x)+isin(2x)) =−(e^(−x) /5)(1+2i)(cos(2x)+isin(2x)) =−(e^(−x) /5){cos(2x)+isin(2x)+2icos(2x)−2sin(2x)} ⇒ v_1 =−(2/5)e^(−x) (cos(2x)−2sin(2x)) V_2 =∫ (W_2 /W)dx =∫((6e^(−2x) cos(2x)dx)/(−3e^(−x) ))dx =−2∫ e^(−x) cos(2x)dx =(2/5)e^(−x) (cos(2x)−2sin(2x)) ⇒ y_p =u_1 v_1 +u_2 v_2 =−(2/5)(cos(2x)−2sin(2x))+(2/5)e^(−3x) (cos(2x)−2sin(2x)) =(−(2/5)+(2/5)e^(−3x) )cos(2x)+((4/5)−(4/5)e^(−3x) )sin(2x) general solution is y =y_h +y_p =ae^x +be^(−2x) +(−(2/5)+(2/5)e^(−3x) )cos(2x) +(4/5)(1−e^(−3x) )sin(2x)
$$\left.\mathrm{2}\right)\:\mathrm{y}^{''} \:+\mathrm{y}−\mathrm{2}=\mathrm{6cos}\left(\mathrm{2x}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{r}−\mathrm{2}=\mathrm{0}\:\rightarrow\Delta=\mathrm{9}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{2}}=\mathrm{1}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{3}}{\mathrm{2}}=−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{−\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{2e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} \:=−\mathrm{3e}^{−\mathrm{x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\mathrm{6cos}\left(\mathrm{2x}\right)\:\:\:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{6e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{−\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{2e}^{−\mathrm{x}} \:\:\:\:\:\mathrm{6cos}\left(\mathrm{2x}\right)}\end{vmatrix}=\mathrm{6e}^{−\mathrm{2x}} \mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$\mathrm{V}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=−\mathrm{6}\int\:\:\frac{\mathrm{e}^{−\mathrm{2x}} \mathrm{cos}\left(\mathrm{2x}\right)}{−\mathrm{3e}^{−\mathrm{x}} }\mathrm{dx}\:=\mathrm{2}\int\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\:\mathrm{Re}\left(\int\:\mathrm{e}^{−\mathrm{x}+\mathrm{2ix}} \mathrm{dx}\right)\:\mathrm{and}\:\int\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{2i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2i}}\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right)\:=−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{5}}\left(\mathrm{1}+\mathrm{2i}\right)\left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right) \\ $$$$=−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{5}}\left\{\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)+\mathrm{2icos}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{2}}{\mathrm{5}}\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right) \\ $$$$\mathrm{V}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\frac{\mathrm{6e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}}{−\mathrm{3e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=−\mathrm{2}\int\:\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{5}}\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right)+\frac{\mathrm{2}}{\mathrm{5}}\mathrm{e}^{−\mathrm{3x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right) \\ $$$$=\left(−\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}}\mathrm{e}^{−\mathrm{3x}} \right)\mathrm{cos}\left(\mathrm{2x}\right)+\left(\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{5}}\mathrm{e}^{−\mathrm{3x}} \right)\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} +\mathrm{y}_{\mathrm{p}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{−\mathrm{2x}} \:+\left(−\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}}\mathrm{e}^{−\mathrm{3x}} \right)\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$+\frac{\mathrm{4}}{\mathrm{5}}\left(\mathrm{1}−\mathrm{e}^{−\mathrm{3x}} \right)\mathrm{sin}\left(\mathrm{2x}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *