Question Number 130943 by help last updated on 30/Jan/21
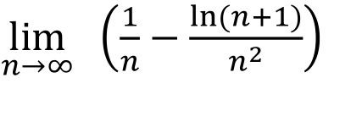
Commented by Dwaipayan Shikari last updated on 30/Jan/21

$$\mathrm{0} \\ $$
Commented by help last updated on 30/Jan/21
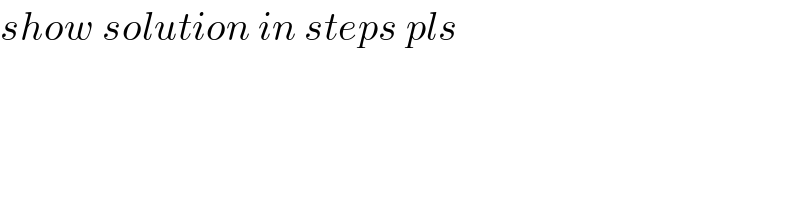
$${show}\:{solution}\:{in}\:{steps}\:{pls} \\ $$
Answered by mathmax by abdo last updated on 30/Jan/21
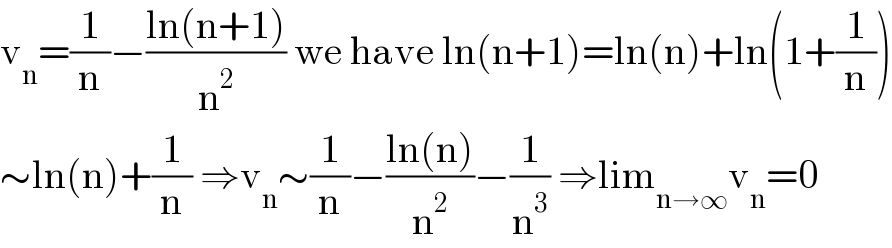
$$\mathrm{v}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{ln}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{n}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{n}+\mathrm{1}\right)=\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$\sim\mathrm{ln}\left(\mathrm{n}\right)+\frac{\mathrm{1}}{\mathrm{n}}\:\Rightarrow\mathrm{v}_{\mathrm{n}} \sim\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \mathrm{v}_{\mathrm{n}} =\mathrm{0} \\ $$
