Question Number 130946 by help last updated on 30/Jan/21
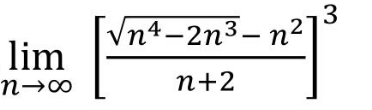
Answered by mathmax by abdo last updated on 30/Jan/21
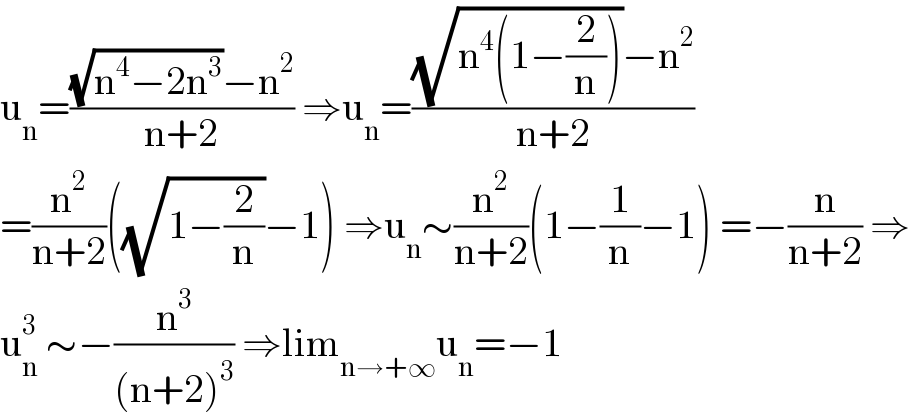
$$\mathrm{u}_{\mathrm{n}} =\frac{\sqrt{\mathrm{n}^{\mathrm{4}} −\mathrm{2n}^{\mathrm{3}} }−\mathrm{n}^{\mathrm{2}} }{\mathrm{n}+\mathrm{2}}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\sqrt{\mathrm{n}^{\mathrm{4}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{n}}\right)}−\mathrm{n}^{\mathrm{2}} }{\mathrm{n}+\mathrm{2}} \\ $$$$=\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}+\mathrm{2}}\left(\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{n}}}−\mathrm{1}\right)\:\Rightarrow\mathrm{u}_{\mathrm{n}} \sim\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}+\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}\right)\:=−\frac{\mathrm{n}}{\mathrm{n}+\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} ^{\mathrm{3}} \:\sim−\frac{\mathrm{n}^{\mathrm{3}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{3}} }\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =−\mathrm{1} \\ $$
Answered by malwan last updated on 31/Jan/21
![lim_(x→∞) [((n^4 −2n^3 −n^4 )/((n+2)((√(n^4 −2n^3 ))+n^2 )))]^3 = lim_(x→∞) [((−2n^3 )/((n+2)n^2 ((√(1−(2/n))) +1)))]^3 ≈lim_(x→∞) [((−2n^3 )/((n^3 +2n^2 )×2))]^3 =(((−2)/2))^3 =−1](https://www.tinkutara.com/question/Q130962.png)
$$\underset{{x}\rightarrow\infty} {{lim}}\:\left[\frac{{n}^{\mathrm{4}} −\mathrm{2}{n}^{\mathrm{3}} −{n}^{\mathrm{4}} }{\left({n}+\mathrm{2}\right)\left(\sqrt{{n}^{\mathrm{4}} −\mathrm{2}{n}^{\mathrm{3}} }+{n}^{\mathrm{2}} \right)}\right]^{\mathrm{3}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {{lim}}\:\left[\frac{−\mathrm{2}{n}^{\mathrm{3}} }{\left({n}+\mathrm{2}\right){n}^{\mathrm{2}} \left(\sqrt{\mathrm{1}−\frac{\mathrm{2}}{{n}}}\:+\mathrm{1}\right)}\right]^{\mathrm{3}} \\ $$$$\approx\underset{{x}\rightarrow\infty} {{lim}}\:\left[\frac{−\mathrm{2}{n}^{\mathrm{3}} }{\left({n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} \right)×\mathrm{2}}\right]^{\mathrm{3}} =\left(\frac{−\mathrm{2}}{\mathrm{2}}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$
