Menu Close

Question-130978

Tinku Tara 0 Comments
Pin




Question Number 130978 by I want to learn more last updated on 31/Jan/21
Commented by I want to learn more last updated on 31/Jan/21
The question start this way: A spring of negligible mass is clamped vertically as shown in the figure. A 2kg ....
$$\mathrm{The}\:\mathrm{question}\:\mathrm{start}\:\mathrm{this}\:\mathrm{way}: \\ $$$$\:\:\:\mathrm{A}\:\mathrm{spring}\:\mathrm{of}\:\mathrm{negligible}\:\mathrm{mass}\:\mathrm{is}\:\mathrm{clamped}\:\mathrm{vertically}\:\mathrm{as}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{figure}.\:\:\mathrm{A}\:\:\mathrm{2kg}\:\:\:…. \\ $$
Commented by mr W last updated on 31/Jan/21
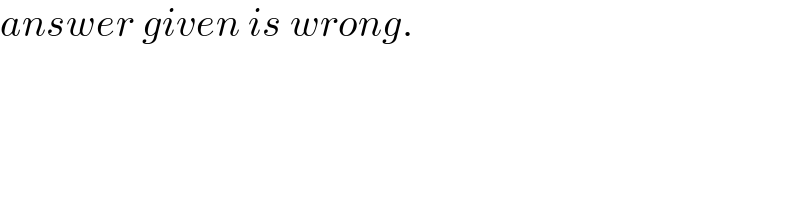
answer given is wrong.
$${answer}\:{given}\:{is}\:{wrong}. \\ $$
Commented by I want to learn more last updated on 31/Jan/21
Please help me sir. Thanks.
$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir}.\:\mathrm{Thanks}. \\ $$
Commented by I want to learn more last updated on 31/Jan/21
Sir, when you are chanced, please help me.
$$\mathrm{Sir},\:\mathrm{when}\:\mathrm{you}\:\mathrm{are}\:\mathrm{chanced},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}. \\ $$
Commented by Tawa11 last updated on 14/Sep/21
nice
$$\mathrm{nice} \\ $$
Answered by mr W last updated on 31/Jan/21
Commented by mr W last updated on 31/Jan/21
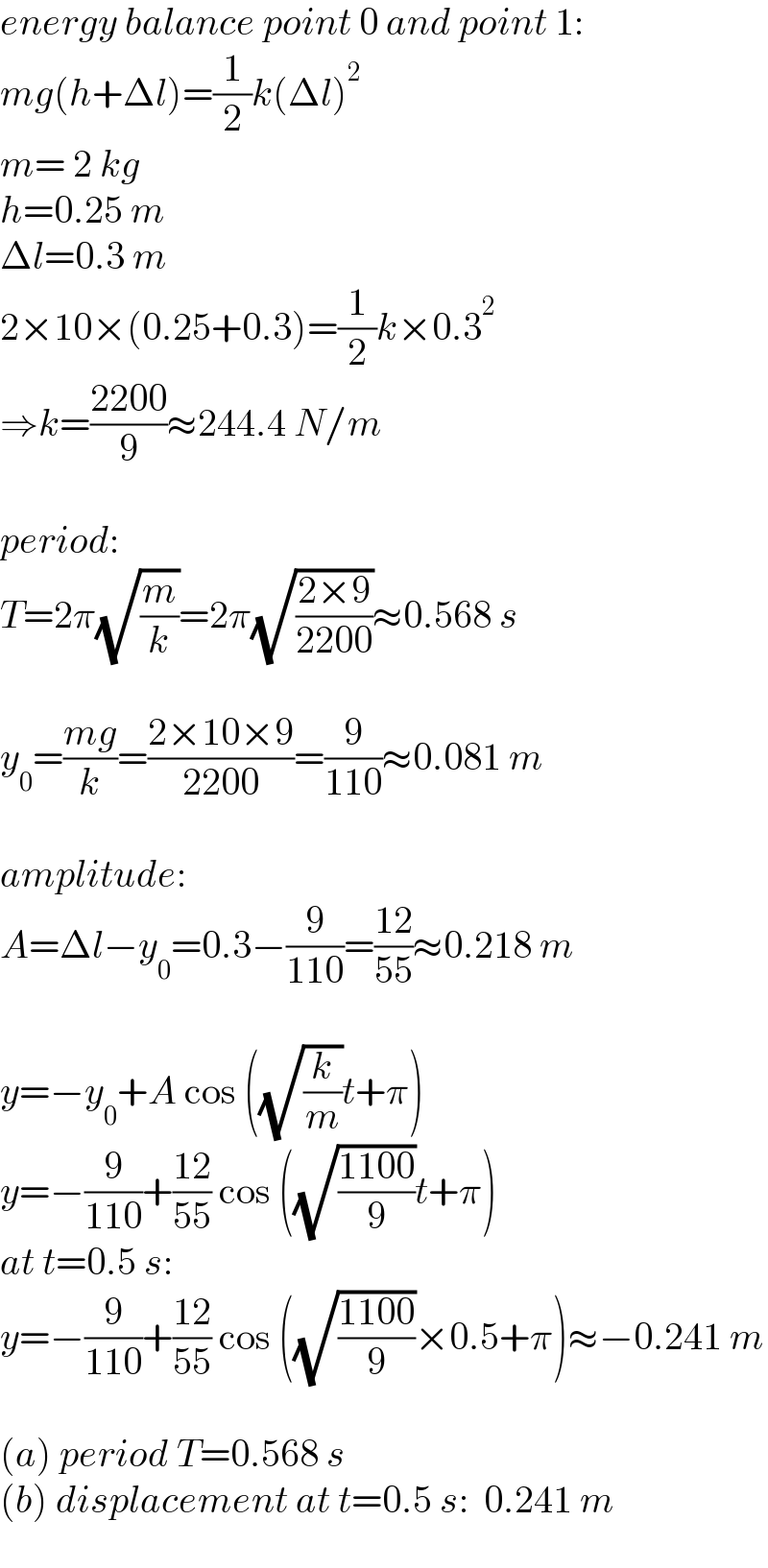
energy balance point 0 and point 1: mg(h+Δl)=(1/2)k(Δl)^2 m= 2 kg h=0.25 m Δl=0.3 m 2×10×(0.25+0.3)=(1/2)k×0.3^2 ⇒k=((2200)/9)≈244.4 N/m period: T=2π(√(m/k))=2π(√((2×9)/(2200)))≈0.568 s y_0 =((mg)/k)=((2×10×9)/(2200))=(9/(110))≈0.081 m amplitude: A=Δl−y_0 =0.3−(9/(110))=((12)/(55))≈0.218 m y=−y_0 +A cos ((√(k/m))t+π) y=−(9/(110))+((12)/(55)) cos ((√((1100)/9))t+π) at t=0.5 s: y=−(9/(110))+((12)/(55)) cos ((√((1100)/9))×0.5+π)≈−0.241 m (a) period T=0.568 s (b) displacement at t=0.5 s: 0.241 m
$${energy}\:{balance}\:{point}\:\mathrm{0}\:{and}\:{point}\:\mathrm{1}: \\ $$$${mg}\left({h}+\Delta{l}\right)=\frac{\mathrm{1}}{\mathrm{2}}{k}\left(\Delta{l}\right)^{\mathrm{2}} \\ $$$${m}=\:\mathrm{2}\:{kg} \\ $$$${h}=\mathrm{0}.\mathrm{25}\:{m} \\ $$$$\Delta{l}=\mathrm{0}.\mathrm{3}\:{m} \\ $$$$\mathrm{2}×\mathrm{10}×\left(\mathrm{0}.\mathrm{25}+\mathrm{0}.\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}{k}×\mathrm{0}.\mathrm{3}^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{2200}}{\mathrm{9}}\approx\mathrm{244}.\mathrm{4}\:{N}/{m} \\ $$$$ \\ $$$${period}: \\ $$$${T}=\mathrm{2}\pi\sqrt{\frac{{m}}{{k}}}=\mathrm{2}\pi\sqrt{\frac{\mathrm{2}×\mathrm{9}}{\mathrm{2200}}}\approx\mathrm{0}.\mathrm{568}\:{s} \\ $$$$ \\ $$$${y}_{\mathrm{0}} =\frac{{mg}}{{k}}=\frac{\mathrm{2}×\mathrm{10}×\mathrm{9}}{\mathrm{2200}}=\frac{\mathrm{9}}{\mathrm{110}}\approx\mathrm{0}.\mathrm{081}\:{m} \\ $$$$ \\ $$$${amplitude}: \\ $$$${A}=\Delta{l}−{y}_{\mathrm{0}} =\mathrm{0}.\mathrm{3}−\frac{\mathrm{9}}{\mathrm{110}}=\frac{\mathrm{12}}{\mathrm{55}}\approx\mathrm{0}.\mathrm{218}\:{m} \\ $$$$ \\ $$$${y}=−{y}_{\mathrm{0}} +{A}\:\mathrm{cos}\:\left(\sqrt{\frac{{k}}{{m}}}{t}+\pi\right) \\ $$$${y}=−\frac{\mathrm{9}}{\mathrm{110}}+\frac{\mathrm{12}}{\mathrm{55}}\:\mathrm{cos}\:\left(\sqrt{\frac{\mathrm{1100}}{\mathrm{9}}}{t}+\pi\right) \\ $$$${at}\:{t}=\mathrm{0}.\mathrm{5}\:{s}: \\ $$$${y}=−\frac{\mathrm{9}}{\mathrm{110}}+\frac{\mathrm{12}}{\mathrm{55}}\:\mathrm{cos}\:\left(\sqrt{\frac{\mathrm{1100}}{\mathrm{9}}}×\mathrm{0}.\mathrm{5}+\pi\right)\approx−\mathrm{0}.\mathrm{241}\:{m} \\ $$$$ \\ $$$$\left({a}\right)\:{period}\:{T}=\mathrm{0}.\mathrm{568}\:{s} \\ $$$$\left({b}\right)\:{displacement}\:{at}\:{t}=\mathrm{0}.\mathrm{5}\:{s}:\:\:\mathrm{0}.\mathrm{241}\:{m} \\ $$
Commented by I want to learn more last updated on 31/Jan/21
Wow, i really appreciate sir.
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *