Question Number 131027 by Algoritm last updated on 31/Jan/21
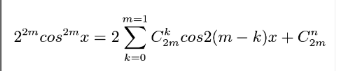
Answered by mathmax by abdo last updated on 31/Jan/21
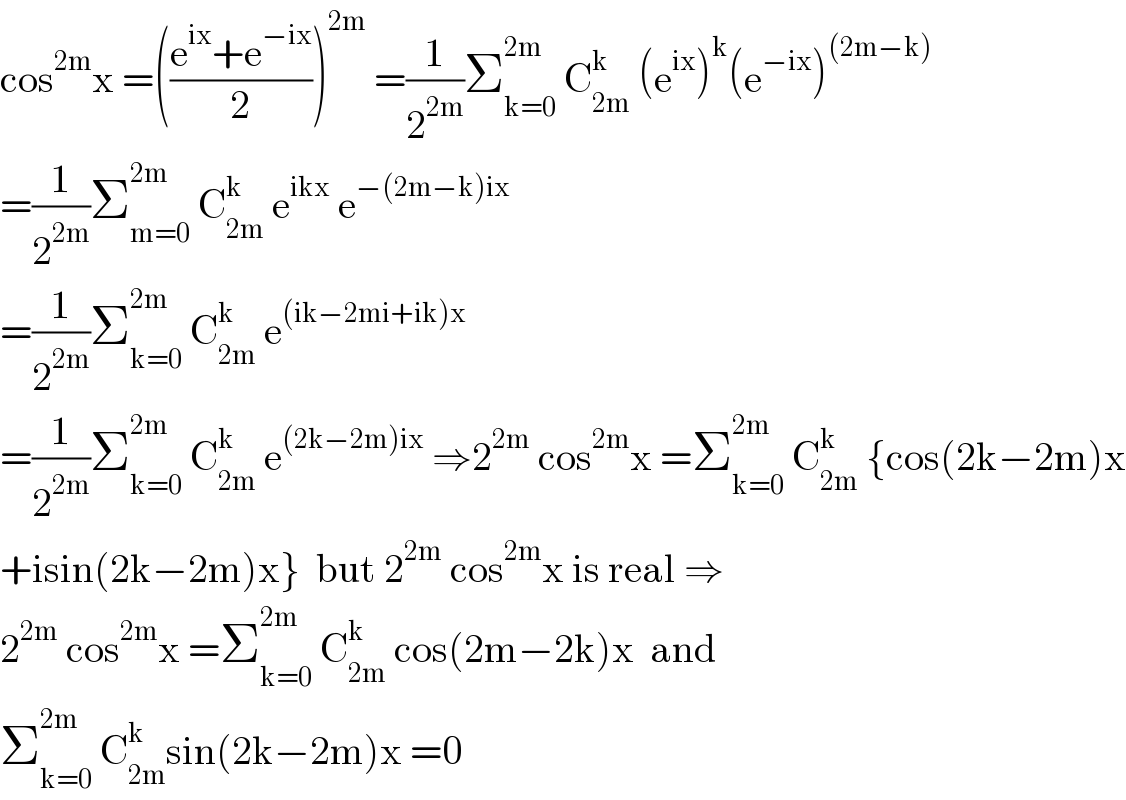
$$\mathrm{cos}^{\mathrm{2m}} \mathrm{x}\:=\left(\frac{\mathrm{e}^{\mathrm{ix}} +\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{2m}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2m}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(\mathrm{e}^{−\mathrm{ix}} \right)^{\left(\mathrm{2m}−\mathrm{k}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2m}} }\sum_{\mathrm{m}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{e}^{−\left(\mathrm{2m}−\mathrm{k}\right)\mathrm{ix}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2m}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\mathrm{e}^{\left(\mathrm{ik}−\mathrm{2mi}+\mathrm{ik}\right)\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2m}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\mathrm{e}^{\left(\mathrm{2k}−\mathrm{2m}\right)\mathrm{ix}} \:\Rightarrow\mathrm{2}^{\mathrm{2m}} \:\mathrm{cos}^{\mathrm{2m}} \mathrm{x}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}\:} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\left\{\mathrm{cos}\left(\mathrm{2k}−\mathrm{2m}\right)\mathrm{x}\right. \\ $$$$\left.+\mathrm{isin}\left(\mathrm{2k}−\mathrm{2m}\right)\mathrm{x}\right\}\:\:\mathrm{but}\:\mathrm{2}^{\mathrm{2m}} \:\mathrm{cos}^{\mathrm{2m}} \mathrm{x}\:\mathrm{is}\:\mathrm{real}\:\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{2m}} \:\mathrm{cos}^{\mathrm{2m}} \mathrm{x}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}} \:\mathrm{cos}\left(\mathrm{2m}−\mathrm{2k}\right)\mathrm{x}\:\:\mathrm{and} \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2m}} \:\mathrm{C}_{\mathrm{2m}} ^{\mathrm{k}\:} \mathrm{sin}\left(\mathrm{2k}−\mathrm{2m}\right)\mathrm{x}\:=\mathrm{0} \\ $$
