Question-13141

Question Number 13141 by tawa tawa last updated on 15/May/17

Commented by RasheedSindhi last updated on 15/May/17

Mr tawa tawa, you are requested to use bigger font.I felt much difficulity to read this question. (I made screen shot of your question and then make it bigger with my fingers!)

$$\mathrm{Mr}\:\mathrm{tawa}\:\mathrm{tawa},\:\mathrm{you}\:\mathrm{are}\:\mathrm{requested} \\ $$$$\mathrm{to}\:\mathrm{use}\:\mathrm{bigger}\:\mathrm{font}.\mathrm{I}\:\mathrm{felt}\:\mathrm{much} \\ $$$$\mathrm{difficulity}\:\mathrm{to}\:\mathrm{read}\:\mathrm{this}\:\mathrm{question}. \\ $$$$\left(\mathrm{I}\:\mathrm{made}\:\mathrm{screen}\:\mathrm{shot}\:\mathrm{of}\:\mathrm{your}\:\mathrm{question}\:\right. \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{make}\:\mathrm{it}\:\mathrm{bigger}\:\mathrm{with} \\ $$$$\left.\mathrm{my}\:\mathrm{fingers}!\right) \\ $$

Commented by tawa tawa last updated on 15/May/17

Sorry for the stress sir. God bless you sir. But am a miss

$$\mathrm{Sorry}\:\mathrm{for}\:\mathrm{the}\:\mathrm{stress}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{But}\:\mathrm{am}\:\mathrm{a}\:\mathrm{miss} \\ $$

Commented by RasheedSindhi last updated on 15/May/17

$$\mathrm{Sorry}\:\mathrm{miss}\:\mathrm{tawa}\:\mathrm{tawa}! \\ $$

Answered by RasheedSindhi last updated on 15/May/17

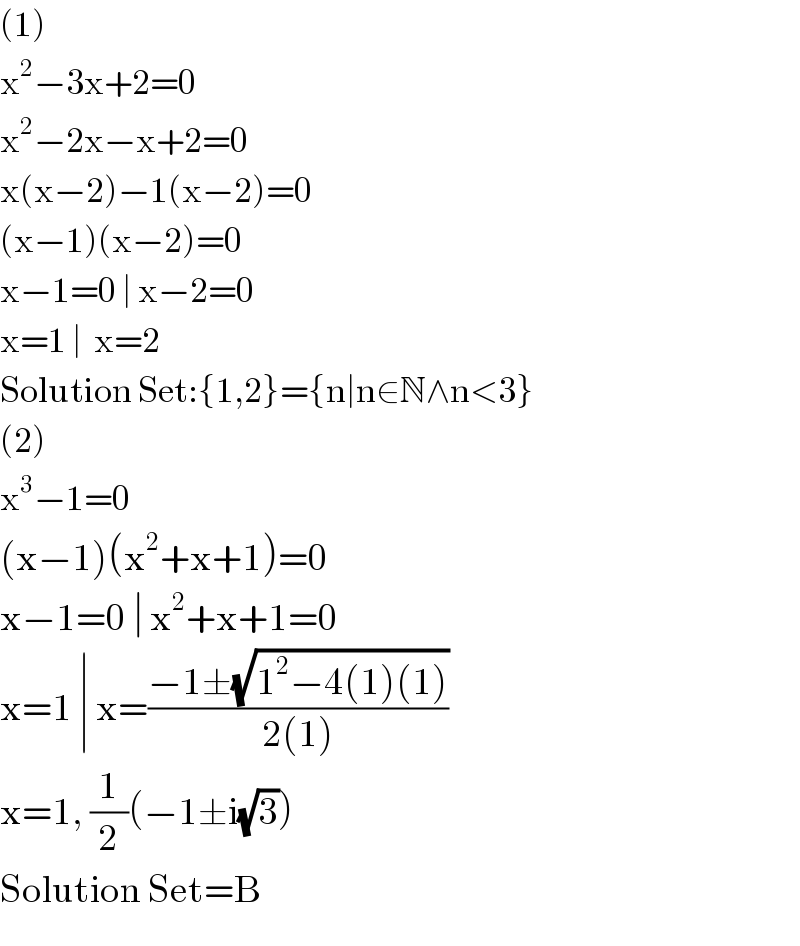
(1) x^2 −3x+2=0 x^2 −2x−x+2=0 x(x−2)−1(x−2)=0 (x−1)(x−2)=0 x−1=0 ∣ x−2=0 x=1 ∣ x=2 Solution Set:{1,2}={n∣n∈N∧n<3} (2) x^3 −1=0 (x−1)(x^2 +x+1)=0 x−1=0 ∣ x^2 +x+1=0 x=1 ∣ x=((−1±(√(1^2 −4(1)(1))))/(2(1))) x=1, (1/2)(−1±i(√3)) Solution Set=B

$$\left(\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{x}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}\left(\mathrm{x}−\mathrm{2}\right)−\mathrm{1}\left(\mathrm{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{x}−\mathrm{1}=\mathrm{0}\:\mid\:\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{1}\:\mid\:\:\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{Solution}\:\mathrm{Set}:\left\{\mathrm{1},\mathrm{2}\right\}=\left\{\mathrm{n}\mid\mathrm{n}\in\mathbb{N}\wedge\mathrm{n}<\mathrm{3}\right\} \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{x}−\mathrm{1}=\mathrm{0}\:\mid\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{1}\:\mid\:\mathrm{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{1}\right)} \\ $$$$\mathrm{x}=\mathrm{1},\:\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{Solution}\:\mathrm{Set}=\mathrm{B} \\ $$

Commented by tawa tawa last updated on 15/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply